题目内容
在数列{an}中，对任意n∈N*，都有an+1-2an=0，则
=________．
分析：根据题意可得此数列为等比数列，且公比q=2，根据等比数列的通项公式，把要求的式子化为
=
，运算可得结果．解答：由于在数列{an}中，对任意n∈N*，都有an+1-2an=0，故此数列为等比数列，且公比q=2，
故
===，故答案为：
．点评：本题考查等比数列的定义和性质，等比数列的通项公式，把要求的式子化为
，是解题的关键． 
练习册系列答案
相关题目
，都有
（k为常数），则称{an}为“等差比数列”. 下面对“等差比数列”的判断： ①k不可能为0；②等差数列一定是等差比数列；③等比数列一定是等差比数列；④通项公式为
的数列一定是等差比数列，其中正确的判断为（ ）
=k(k为常数)，则称数列{an}为“等差比数列”，下面对“等差比数列”判断：①k不可能为0；②等差数列一定是等差比数列；③等比数列一定是等差比数列；④通项公式为an=a·bn+c(a≠0，b≠0、1)的数列一定是等差比数列，其中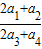判断正确的是
= ．