题目内容
等比数列的前n项,前2n项,前3n项的和分别为A,B,C,则
- A.A+B=C
- B.B2=AC
- C.(A+B)-C=B2
- D.A2+B2=A(B+C)
D
因为若数列{an}是等比数列,Sn为其前n项和,所以Sn,S2n-Sn,S3n-S2n仍成等比数列.
由Sn=A,S2n-Sn=B-A,S3n-S2n=C-B,得(B-A)2=A·(C-B),化简得,A2+B2=A(B+C).
因为若数列{an}是等比数列,Sn为其前n项和,所以Sn,S2n-Sn,S3n-S2n仍成等比数列.
由Sn=A,S2n-Sn=B-A,S3n-S2n=C-B,得(B-A)2=A·(C-B),化简得,A2+B2=A(B+C).

练习册系列答案
相关题目
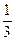 )是函数
)是函数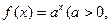 且
且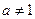 )的图象上一点,等比数列
)的图象上一点,等比数列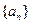 的前n项和为
的前n项和为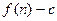 ,数列
,数列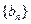
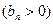 的首项为c,且前n项和
的首项为c,且前n项和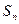 满足
满足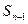 =
=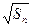 +
+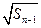 (n
(n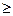 2).
2).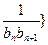 前n项和为
前n项和为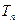 ,问
,问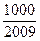 的最小正整数n是多少?
的最小正整数n是多少?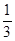 )是函数
)是函数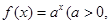 且
且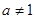 )的图象上一点,等比数列
)的图象上一点,等比数列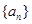 的前n项和为
的前n项和为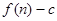 ,数列
,数列
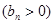 的首项为c,且前n项和
的首项为c,且前n项和 满足
满足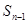 =
=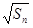 +
+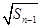 (n
(n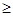 2).
2).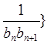 前n项和为
前n项和为 ,问
,问 的最小正整数n是多少?
的最小正整数n是多少?