题目内容
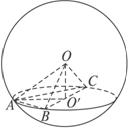
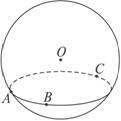
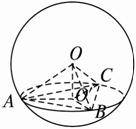
如图A、B、C是球面三点,且OA、OB、OC两两垂直,若P是球O的大圆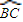 的中点,O为球心,则直线AP与OB所成角的大小为 .
的中点,O为球心,则直线AP与OB所成角的大小为 .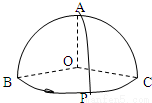
【答案】分析:利用空间向量来求,建立空间直角坐标系,把异面直线AP与OB所成角转化为向量 与
与 所成角,再利用向量的夹角公式计算即可.
所成角,再利用向量的夹角公式计算即可.
解答:解:∵OA、OB、OC两两垂直,
以OB所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立空间直角坐标系,
设球半径为1,则B(1,0,0),C(0,1,0),A(0,0,1)P( ,
, ,0)
,0)
∴ =(
=( ,
, ,-1),
,-1), =(1,0,0)
=(1,0,0)
cos< ,
, >=
>= =
=

∴向量 与
与 所成角为
所成角为 ,也即直线AP与OB所成角为
,也即直线AP与OB所成角为
点评:本题主要考查了利用空间向量求异面直线所成角的大小,属于空间向量的应用.
 与
与 所成角,再利用向量的夹角公式计算即可.
所成角,再利用向量的夹角公式计算即可.解答:解:∵OA、OB、OC两两垂直,
以OB所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立空间直角坐标系,
设球半径为1,则B(1,0,0),C(0,1,0),A(0,0,1)P(
 ,
, ,0)
,0)∴
 =(
=( ,
, ,-1),
,-1), =(1,0,0)
=(1,0,0)cos<
 ,
, >=
>= =
=

∴向量
 与
与 所成角为
所成角为 ,也即直线AP与OB所成角为
,也即直线AP与OB所成角为
点评:本题主要考查了利用空间向量求异面直线所成角的大小,属于空间向量的应用.

练习册系列答案
相关题目
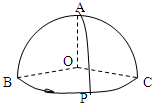 如图A、B、C是球面三点,且OA、OB、OC两两垂直,若P是球O的大圆
如图A、B、C是球面三点,且OA、OB、OC两两垂直,若P是球O的大圆