题目内容
已知 ,设函数
,设函数 .
.
(Ⅰ)当 ,求函数f(x)的值域;
,求函数f(x)的值域;
(Ⅱ)当 时,若f(x)=8,求函数
时,若f(x)=8,求函数 的值.
的值.
解:(I)∵ =5
=5 sinxcosx+2cos2x,
sinxcosx+2cos2x, =sin2x+4cos2x
=sin2x+4cos2x
∴ =5
=5 sinxcosx+2cos2x+sin2x+4cos2x+
sinxcosx+2cos2x+sin2x+4cos2x+
= sin2x+3(1+cos2x)+
sin2x+3(1+cos2x)+ (1-cos2x)+
(1-cos2x)+
= sin2x+
sin2x+ cos2x+5=5sin(2x+
cos2x+5=5sin(2x+ )+5
)+5
∵ ,∴2x+
,∴2x+ ∈[
∈[ ,
, ]
]
因此,- ≤sin(2x+
≤sin(2x+ )≤1,可得函数f(x)的值域是[
)≤1,可得函数f(x)的值域是[ ,10].…(6分)
,10].…(6分)
(Ⅱ)由(I)得5sin(2x+ )+5=8,得sin(2x+
)+5=8,得sin(2x+ )=
)=
∵ ,∴2x+
,∴2x+ ∈[
∈[ ,
, ]
]
∴ ,…(10分)
,…(10分)
∴sin2x=sin[(2x+ )-
)- ]=
]= •
• -(-
-(- )•
)• =
=
因此, =
= .…(12分)
.…(12分)
分析:(I)根据向量数量积的坐标公式和模的公式代入,再用二倍角的正、余弦公式和辅助角公式化简,得f(x)=5sin(2x+ )+5,根据
)+5,根据 得2x+
得2x+ ∈[
∈[ ,
, ],结合正弦函数的图象与性质,可得函数f(x)的值域;
],结合正弦函数的图象与性质,可得函数f(x)的值域;
(II)根据f(x)=8,得sin(2x+ )=
)= ,再利用配角公式算出sin2x的值,而
,再利用配角公式算出sin2x的值,而 =5sin2x+5,将sin2x代入即得
=5sin2x+5,将sin2x代入即得 的值..
的值..
点评:本题以向量的数量积运算和模的计算为载体,考查了三角函数的降次公式、辅助角公式和三角函数的图象与性质等知识,属于中档题.
 =5
=5 sinxcosx+2cos2x,
sinxcosx+2cos2x, =sin2x+4cos2x
=sin2x+4cos2x∴
 =5
=5 sinxcosx+2cos2x+sin2x+4cos2x+
sinxcosx+2cos2x+sin2x+4cos2x+
=
 sin2x+3(1+cos2x)+
sin2x+3(1+cos2x)+ (1-cos2x)+
(1-cos2x)+
=
 sin2x+
sin2x+ cos2x+5=5sin(2x+
cos2x+5=5sin(2x+ )+5
)+5∵
 ,∴2x+
,∴2x+ ∈[
∈[ ,
, ]
]因此,-
 ≤sin(2x+
≤sin(2x+ )≤1,可得函数f(x)的值域是[
)≤1,可得函数f(x)的值域是[ ,10].…(6分)
,10].…(6分)(Ⅱ)由(I)得5sin(2x+
 )+5=8,得sin(2x+
)+5=8,得sin(2x+ )=
)=
∵
 ,∴2x+
,∴2x+ ∈[
∈[ ,
, ]
]∴
 ,…(10分)
,…(10分)∴sin2x=sin[(2x+
 )-
)- ]=
]= •
• -(-
-(- )•
)• =
=
因此,
 =
= .…(12分)
.…(12分)分析:(I)根据向量数量积的坐标公式和模的公式代入,再用二倍角的正、余弦公式和辅助角公式化简,得f(x)=5sin(2x+
 )+5,根据
)+5,根据 得2x+
得2x+ ∈[
∈[ ,
, ],结合正弦函数的图象与性质,可得函数f(x)的值域;
],结合正弦函数的图象与性质,可得函数f(x)的值域;(II)根据f(x)=8,得sin(2x+
 )=
)= ,再利用配角公式算出sin2x的值,而
,再利用配角公式算出sin2x的值,而 =5sin2x+5,将sin2x代入即得
=5sin2x+5,将sin2x代入即得 的值..
的值..点评:本题以向量的数量积运算和模的计算为载体,考查了三角函数的降次公式、辅助角公式和三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
 ,设函数
,设函数
 ,求函数f(x)的值域;
,求函数f(x)的值域; 时,若f(x)=8,求函数
时,若f(x)=8,求函数 的值;
的值; 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.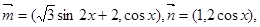 设函数
设函数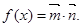
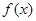 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;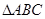 中
中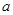 、
、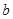 、
、 分别是角
分别是角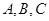 的对边,若
的对边,若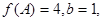
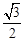 ,求
,求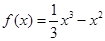 .
.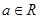 ,设函数
,设函数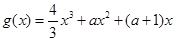 的单调递减区间为
的单调递减区间为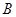 ,且
,且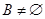 ,
,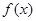 的单调递减区间为
的单调递减区间为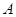 ,若
,若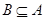 ,求
,求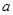 的取值范围.
的取值范围.