题目内容
如图,分别是直三棱柱ABC-A1B1C1直观图及其正视图、俯视图、侧视图.
(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求证:MN⊥平面A1BC;
(Ⅲ)求二面角A-A1B-C的大小.
分析:由三视图可知三棱柱的底面是一个直角边为a的等腰直角三角形,高为a,由于在C点出现三线垂直,故我们可以以C为原点,分别以CB、CC1、CA为x、y、z轴建立空间坐标系,利用向量法解题.
(1)要证MN∥平面ACC1A1,即证直线MN的方向向量与平面ACC1A1的法向量垂直;
(2)要证MN⊥平面A1BC,即证直线MN的方向向量与平面A1BC的法向量平行;
(3)二面角A-A1B-C的大小,即求平面A1BA的法向量与平面A1BC的法向量的夹角(或其补角)
(1)要证MN∥平面ACC1A1,即证直线MN的方向向量与平面ACC1A1的法向量垂直;
(2)要证MN⊥平面A1BC,即证直线MN的方向向量与平面A1BC的法向量平行;
(3)二面角A-A1B-C的大小,即求平面A1BA的法向量与平面A1BC的法向量的夹角(或其补角)
解答: 解:(Ⅰ)以C为原点,分别以CB、CC1、CA为x、y、z轴建立坐标系,
解:(Ⅰ)以C为原点,分别以CB、CC1、CA为x、y、z轴建立坐标系,
则AC=BC=CC1=a,A(0,0,a),C1(0,a,0),
M(
,
,
),N(
, a , 0),
AC1=(0,a,-a),
=(0 ,
, -
),
∴
=2
,AC1∥MN,
故MN∥平面ACC1A1.
(Ⅱ)∵A1(0,a,a)、B(a,0,0),
∴
=(a , -a , -a);
又
•
=0×a-a×
-a×(-
)=0,
•
=0×a+0×
+0×(-
)=0,
∴MN⊥A1B,MN⊥CB,
又∵CB∩A1B=B,CB,A1B?平面A1BC
∴MN⊥平面A1BC.
(Ⅲ)作CH⊥AB于H点,
∵平面ABC⊥平面ABB1A1,
∴CH⊥平面A1BA,
故平面A1BA的一个法向量为
=(
, 0 ,
),
而平面A1BC的一个法向量为
=(0 ,
, -
),
∴cos?
,
>=
=
=-
,
故二面角A-A1B-C的大小为
.
 解:(Ⅰ)以C为原点,分别以CB、CC1、CA为x、y、z轴建立坐标系,
解:(Ⅰ)以C为原点,分别以CB、CC1、CA为x、y、z轴建立坐标系,则AC=BC=CC1=a,A(0,0,a),C1(0,a,0),
M(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
AC1=(0,a,-a),
| MN |
| a |
| 2 |
| a |
| 2 |
∴
| AC1 |
| MN |
故MN∥平面ACC1A1.
(Ⅱ)∵A1(0,a,a)、B(a,0,0),
∴
| A1B |
又
| MN |
| A1B |
| a |
| 2 |
| a |
| 2 |
| MN |
| CB |
| a |
| 2 |
| a |
| 2 |
∴MN⊥A1B,MN⊥CB,
又∵CB∩A1B=B,CB,A1B?平面A1BC
∴MN⊥平面A1BC.
(Ⅲ)作CH⊥AB于H点,
∵平面ABC⊥平面ABB1A1,
∴CH⊥平面A1BA,
故平面A1BA的一个法向量为
| CH |
| a |
| 2 |
| a |
| 2 |
而平面A1BC的一个法向量为
| MN |
| a |
| 2 |
| a |
| 2 |
∴cos?
| CH |
| MN |
| ||||
|
|
-
| ||||||||
|
| 1 |
| 2 |
故二面角A-A1B-C的大小为
| π |
| 3 |
点评:根据三视图判断空间几何体的形状,进而求几何的表(侧/底)面积或体积,是高考必考内容,处理的关键是准确判断空间几何体的形状,一般规律是这样的:如果三视图均为三角形,则该几何体必为三棱锥;如果三视图中有两个三角形和一个多边形,则该几何体为N棱锥(N值由另外一个视图的边数确定);如果三视图中有两个为矩形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个为梯形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个三角形和一个圆,则几何体为圆锥.如果三视图中有两个矩形和一个圆,则几何体为圆柱.如果三视图中有两个梯形和一个圆,则几何体为圆台.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
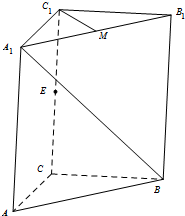 如图所示,直三棱柱ABC-A1B1C1中,CA=CB,∠BCA=90°,E、M分别是CC1、A1B1的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB,∠BCA=90°,E、M分别是CC1、A1B1的中点.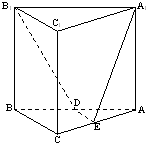 (2008•静安区一模)如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=
(2008•静安区一模)如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=
