题目内容
已知定义在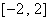 上的奇函数
上的奇函数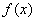 满足:当
满足:当 时,
时,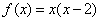 .
.
(1)求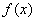 的解析式和值域;
的解析式和值域;
(2)设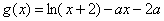 ,其中常数
,其中常数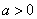 .
.
①试指出函数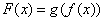 的零点个数;
的零点个数;
②若当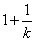 是函数
是函数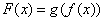 的一个零点时,相应的常数
的一个零点时,相应的常数 记为
记为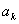 ,其中
,其中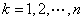 .证明:
.证明: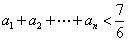 (
( ).
).
解:(1) 为奇函数,
为奇函数,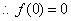 .
.
当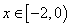 时,
时, ,则
,则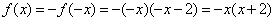 ,
,



 时,
时, ,
, ,
,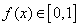 ,
,
 的值域为
的值域为 .
.
(2)①函数 的图象如图
的图象如图 所示,当
所示,当 时,方程
时,方程
有三个实根;当 或
或 时,方程
时,方程 只有一个实
只有一个实
根;当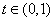 或
或 时,方程
时,方程 有两个实根.
有两个实根.
(法一):由 ,解得
,解得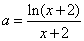 ,
,
 的值域为
的值域为 ,
, 只需研究函数
只需研究函数 在
在 上的图象特征.
上的图象特征.
设 ,
, ,
, ,
,
令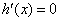 ,得
,得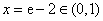 ,
,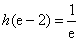 .
.
 当
当 时,
时, ,当
,当 时,
时, ,
,
又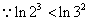 ,即
,即 ,由
,由 ,
, ,得
,得 ,
,

 的大致图象如图
的大致图象如图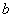 所示.
所示.
根据图象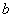 可知,当
可知,当 时,
时,
直线 与函数
与函数 的图像仅有一个交点,则函数
的图像仅有一个交点,则函数
在 上仅有一个零点,记零点为
上仅有一个零点,记零点为 ,则
,则 分别在区间
分别在区间 、
、
 、
、 上,根据图像
上,根据图像 ,方程
,方程 有两个交点,因此
有两个交点,因此
函数 有两个零点.
有两个零点.
类似地,当 时,函数
时,函数 在
在 上仅有零点
上仅有零点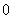 ,因此函数
,因此函数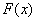 有
有 、
、 、
、 这三个零点.
这三个零点.
当 时,函数
时,函数 在
在 上有两个零点,一个零点是
上有两个零点,一个零点是 ,另一个零点在
,另一个零点在 内,因此函数
内,因此函数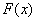 有三个零点.
有三个零点.
当 时,函数
时,函数 在
在 上有两个零点,且这两个零点均在
上有两个零点,且这两个零点均在 内,因此函数
内,因此函数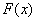 有四个零点.
有四个零点.
当 时,函数
时,函数 在
在 上没有零点,因此函数
上没有零点,因此函数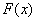 没有零点. …9分
没有零点. …9分
 (法二):
(法二): ,令
,令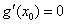 ,得
,得 ,
,
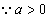 ,
, .
.
当 时,
时, ,当
,当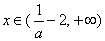 时,
时, ,
,
 当
当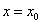 时,
时, 取得极大值
取得极大值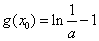 .
.
 (Ⅰ)当
(Ⅰ)当 的极大值
的极大值 ,即
,即 时,函数
时,函数 在区间
在区间 上无零点,因此函数
上无零点,因此函数 无零点.
无零点.
(Ⅱ)当 的极大值
的极大值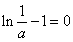 ,即
,即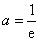 时,
时,
 ,函数
,函数 的图像如图
的图像如图 所示,函数
所示,函数 有零点
有零点 .
.
由图 可知方程
可知方程 有两不等的实根,因此函数
有两不等的实根,因此函数 有两个零点.
有两个零点.
(Ⅲ)当 的极大值
的极大值 且
且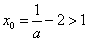 ,
,
即 时,
时, 在
在 上单调递增,因为
上单调递增,因为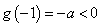 ,
, ,函数
,函数 的图像如图
的图像如图 所示,函数
所示,函数 在
在 存在唯一零点
存在唯一零点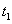 ,其中
,其中 .
.
由图 可知方程
可知方程 有两不等的实根,因此函数
有两不等的实根,因此函数 有两个零点.
有两个零点.
 (Ⅳ)当
(Ⅳ)当 的极大值
的极大值 且
且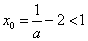 ,
,
即 时:
时:
由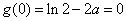 ,得
,得 ,
,
由 ,得
,得 ,
,
根据法一中的证明有 .
.
(ⅰ)当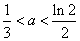 时,
时, ,
,
 ,函数
,函数 的图像如图
的图像如图 所示,
所示,
 函数
函数 在区间
在区间 有唯一零点
有唯一零点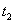 ,其中
,其中 .
.
由图 可知方程
可知方程 有两不等的实根,因此
有两不等的实根,因此
函数 有两个零点.
有两个零点.
(ⅱ)当 时,
时,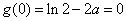 ,
,
 ,函数
,函数 的图像如图
的图像如图 所示,
所示,
函数 在区间
在区间 有唯一零点
有唯一零点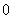 .
.
由图 可知方程
可知方程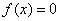 有三个不等的实根,因此函数
有三个不等的实根,因此函数 有三个零点.
有三个零点.
(ⅲ)当 时,
时, ,
, ,函数
,函数 的
的
图像如图 所示,函数
所示,函数 在区间
在区间 有唯一零点
有唯一零点 ,其中
,其中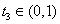 .
.
由图 可知方程
可知方程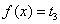 有两个不等的实根,因此函数
有两个不等的实根,因此函数

 有两个零点.
有两个零点.
(ⅳ)当 时,
时, ,
, ,
,
函数 的图像如图
的图像如图 所示,函数
所示,函数 在区间
在区间 有
有
两个零点,分别是 和
和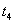 ,其中
,其中 .
.
由图 可知方程
可知方程 有一个实根
有一个实根 ,方程
,方程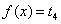
有两个非 的不等实根,因此函数
的不等实根,因此函数 有三个零点.
有三个零点.
(ⅴ)当 时,
时, ,
, ,
,
函数 的图像如图
的图像如图 所示,函数
所示,函数 在区间
在区间 有两个
有两个
零点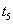 、
、 ,其中
,其中 .
.
由图 可知方程
可知方程 、
、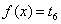 都有两个不等的实根,
都有两个不等的实根,
且这四个根互不相等,因此函数 有四个零点.
有四个零点.
综上可得:
 当
当 时,函数
时,函数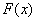 有两个零点
有两个零点
当 、
、 时,函数
时,函数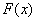 有三个零点;
有三个零点;
当 时,函数
时,函数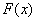 有四个零点;
有四个零点;
当 时,函数
时,函数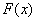 无零点.
无零点.
②因为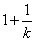 是函数
是函数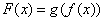 的一个零点,所以有
的一个零点,所以有 ,
,
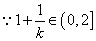 ,
, ,
,
 ,
,

 ,
,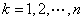 .
.
记 ,
, ,
,
 当
当 时,
时, ,
,
 当
当 时,
时,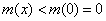 ,即
,即 .
.
故有 ,则
,则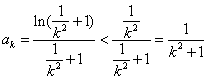
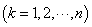 .
.
当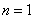 时,
时, ;
;
当 时,
时,
(法一): ,
,
 …
…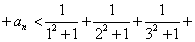 …
…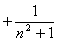

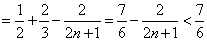 .
.
综上,有 …
… ,
, .
.
(法二):当 时,
时, ;
;
当 时,
时, ,
,
 …
…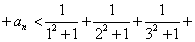 …
…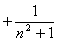

 .
.
综上,有 …
… ,
, .
.

 几何中,有边长为
几何中,有边长为 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值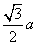 ,类比上述命题,棱长为
,类比上述命题,棱长为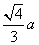 B.
B.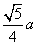 C.
C.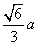 D.
D.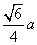
 ,若
,若 ,则
,则 ;
; 与函数
与函数 的图象相同;
的图象相同; ;
;
 的最小正周期为
的最小正周期为 .其中真命题是
.其中真命题是 ,
, B.
B. ,
, D.
D. 为数列
为数列 的前n项和,且对任意
的前n项和,且对任意 都有
都有 ,记
,记 ,
,  与
与 的大小关系为____________.
的大小关系为____________. 在R上恒成立的充分不必要条件是 ( )
在R上恒成立的充分不必要条件是 ( ) B.
B. C.
C. D.
D.
 a,AB⊥AC,D为AA1的中点.
a,AB⊥AC,D为AA1的中点. (Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为
(Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为
 ,则cos2α= .
,则cos2α= . ,则
,则 的值是
的值是