题目内容
△ABC中，AB=3，BC=4，AC=5，将三角形绕AC边旋转一周所成的几何体的体积为
．
| 48π |
| 5 |
| 48π |
| 5 |
分析：如图所示，将此三角形绕AC边旋转一周所成的几何体为两个对底面的上下两个圆锥，其底面半径为三角形斜边上的高，据此即可计算出体积．
解答：解：如图所示：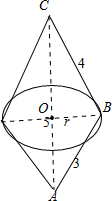
将此三角形绕AC边旋转一周所成的几何体为两个对底面的上下两个圆锥，其底面半径为三角形斜边上的高r=
=
．
∴V=
×π×(
)2×5=
．
故答案为
．
将此三角形绕AC边旋转一周所成的几何体为两个对底面的上下两个圆锥，其底面半径为三角形斜边上的高r=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴V=
| 1 |
| 3 |
| 12 |
| 5 |
| 48π |
| 5 |
故答案为
| 48π |
| 5 |
点评：弄清旋转所得的几何体的形状和掌握圆锥体积的计算公式是解题的关键．
练习册系列答案
一课一练课时达标系列答案
期末宝典单元检测分类复习卷系列答案
相关题目