题目内容
已知F1，F2是椭圆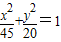
的两个焦点，M是椭圆上的第一象限内的点，且MF1⊥MF2．（1）求△MF1F2的周长；
（2）求点M的坐标．
【答案】分析：（1）先根据椭圆的方程得出长半轴的长，进而得出焦距的长，再由椭圆的定义可得△MF1F2的周长；
（2）设点M坐标为（x，y），在Rt△F1PF2中，由勾股定理结合椭圆的定义，结合三角形的面积可解得y，再代入椭圆的方程，从而求得点M的坐标．
解答：解：椭圆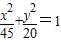
中，长半轴
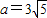，焦距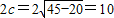
（1）根据椭圆定义，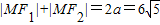
所以，△MF1F2的周长为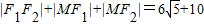
（2）设点M坐标为（x，y）
由MF1⊥MF2得，
，
，
∴
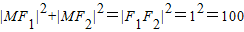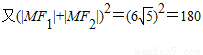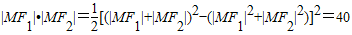
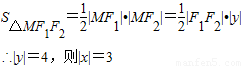
∵M是椭圆上的第一象限内的点，
∴点M坐标为（3，4）．
点评：本题考查椭圆的简单性质和定义，以及勾股定理的应用，属于基础题．
（2）设点M坐标为（x，y），在Rt△F1PF2中，由勾股定理结合椭圆的定义，结合三角形的面积可解得y，再代入椭圆的方程，从而求得点M的坐标．
解答：解：椭圆
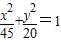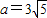中，长半轴，焦距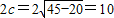（1）根据椭圆定义，
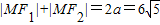
所以，△MF1F2的周长为
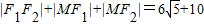
（2）设点M坐标为（x，y）
由MF1⊥MF2得，
，，∴
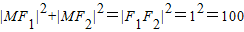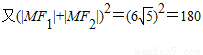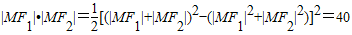
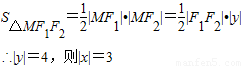
∵M是椭圆上的第一象限内的点，
∴点M坐标为（3，4）．
点评：本题考查椭圆的简单性质和定义，以及勾股定理的应用，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
相关题目