题目内容
若函数f（x）=
在（﹣∞，+∞）上为增函数，实数b的取值范围是 [1，2] ．
考点：
二次函数的性质．
专题：
函数的性质及应用．
分析：
由题意可得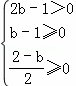 
，解此不等式组求得实数b的取值范围．
解答：
解：∵函数f（x）=在（﹣∞，+∞）上为增函数，∴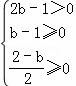
，解得 1≤b≤2，
故实数b的取值范围是[1，2]，
故答案为[1，2]．
点评：
本题主要考查二次函数的性质的应用，得到 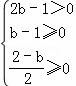，是解题的关键，属于基础题．
练习册系列答案
快捷英语周周练系列答案
相关题目