题目内容
若函数f(x)=ax2-2ax+1-a在R上的函数值恒大于0,则实数a的取值范围是 .
【答案】分析:由于a为二次项系数,故要分a等于和不等于两种情况来讨论,
当a≠0时,根据二次函数的性质,a>0,图象开口向上,且b2-4ac<0时图象始终在x轴上方,即可得出答案;
当a=0时,满足题意.
解答:解:①当a≠0时,根据二次函数与x轴交点性质得出:
b2-4ac<0,且a>0时,不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0,
即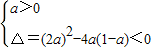 解得 0
解得 0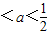
②当a=0时,函数f(x)=ax2-2ax+1-a=1在R上的函数值恒大于0,
故a=0满足题意.
故答案为: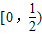
点评:此题主要考查了抛物线与坐标轴的交点性质,熟练掌握其性质是解题关键.
当a≠0时,根据二次函数的性质,a>0,图象开口向上,且b2-4ac<0时图象始终在x轴上方,即可得出答案;
当a=0时,满足题意.
解答:解:①当a≠0时,根据二次函数与x轴交点性质得出:
b2-4ac<0,且a>0时,不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0,
即
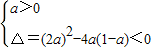 解得 0
解得 0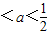
②当a=0时,函数f(x)=ax2-2ax+1-a=1在R上的函数值恒大于0,
故a=0满足题意.
故答案为:
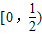
点评:此题主要考查了抛物线与坐标轴的交点性质,熟练掌握其性质是解题关键.

练习册系列答案
相关题目