题目内容
设函数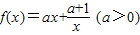 ,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.
,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.(Ⅰ)求a的值;
(Ⅱ)若
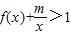 对一切x>0恒成立,求m的取值范围;
对一切x>0恒成立,求m的取值范围;(Ⅲ)若函数h(x)=k-f(x)-g(x)(k∈R)在[m,n]上的值域为[m,n](其中n>m>0),求k的取值范围.
【答案】分析:(Ⅰ)依题意有ax+ =4-x,利用△=0即可求得a的值;
=4-x,利用△=0即可求得a的值;
(Ⅱ)由(Ⅰ)知x+ >1对一切x>0恒成立,转化为m+2>-x2+x对一切x>0恒成立,利用配方法求得-x2+x的最大值即可;
>1对一切x>0恒成立,转化为m+2>-x2+x对一切x>0恒成立,利用配方法求得-x2+x的最大值即可;
(Ⅲ)可求得h(x)=(k-4)- ,易知,h(x)在(0,+∞)是增函数,由方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,列关系式可求得k的取值范围.
,易知,h(x)在(0,+∞)是增函数,由方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,列关系式可求得k的取值范围.
解答:解:(Ⅰ)由条件知:ax+ =4-x,
=4-x,
∴(a+1)x2-4x+a+1=0有且只有一解,…(2分)
∵a>0,
∴△=16-4(a+1)2=0,
∴a=1…(4分)
(Ⅱ)由(Ⅰ)知,f(x)=x+ ,
,
∴x+ >1对一切x>0恒成立,
>1对一切x>0恒成立,
∴m+2>-x2+x对一切x>0恒成立,…(6分)
而-x2+x=- +
+ ≤
≤ ,
,
∴m+2> ,m>-
,m>- …(9分)
…(9分)
(Ⅲ)h(x)=k- -4=(k-4)-
-4=(k-4)- ,
,
易知,h(x)在(0,+∞)是增函数,…(10分)
∴ ,∴m,n是方程(k-4)-
,∴m,n是方程(k-4)- =x的两实根,
=x的两实根,
∴方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,…(12分)
令φ(x)=x2-(k-4)x+2,
则 ⇒k>4+2
⇒k>4+2 .
.
即k的取值范围是(4+2 ,+∞)…(15分)
,+∞)…(15分)
点评:本题考查函数恒成立问题,考查二次函数在闭区间上的最值,考查二次函数有唯一解中判别式的应用,突出转化思想与方程思想的综合运用,属于难题.
 =4-x,利用△=0即可求得a的值;
=4-x,利用△=0即可求得a的值;(Ⅱ)由(Ⅰ)知x+
 >1对一切x>0恒成立,转化为m+2>-x2+x对一切x>0恒成立,利用配方法求得-x2+x的最大值即可;
>1对一切x>0恒成立,转化为m+2>-x2+x对一切x>0恒成立,利用配方法求得-x2+x的最大值即可;(Ⅲ)可求得h(x)=(k-4)-
 ,易知,h(x)在(0,+∞)是增函数,由方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,列关系式可求得k的取值范围.
,易知,h(x)在(0,+∞)是增函数,由方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,列关系式可求得k的取值范围.解答:解:(Ⅰ)由条件知:ax+
 =4-x,
=4-x,∴(a+1)x2-4x+a+1=0有且只有一解,…(2分)
∵a>0,
∴△=16-4(a+1)2=0,
∴a=1…(4分)
(Ⅱ)由(Ⅰ)知,f(x)=x+
 ,
,∴x+
 >1对一切x>0恒成立,
>1对一切x>0恒成立,∴m+2>-x2+x对一切x>0恒成立,…(6分)
而-x2+x=-
 +
+ ≤
≤ ,
,∴m+2>
 ,m>-
,m>- …(9分)
…(9分)(Ⅲ)h(x)=k-
 -4=(k-4)-
-4=(k-4)- ,
,易知,h(x)在(0,+∞)是增函数,…(10分)
∴
 ,∴m,n是方程(k-4)-
,∴m,n是方程(k-4)- =x的两实根,
=x的两实根,∴方程x2-(k-4)x+2=0在(0,+∞)有两不等实根,…(12分)
令φ(x)=x2-(k-4)x+2,
则
 ⇒k>4+2
⇒k>4+2 .
.即k的取值范围是(4+2
 ,+∞)…(15分)
,+∞)…(15分)点评:本题考查函数恒成立问题,考查二次函数在闭区间上的最值,考查二次函数有唯一解中判别式的应用,突出转化思想与方程思想的综合运用,属于难题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
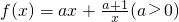 ,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.
,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.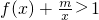 对一切x>0恒成立,求m的取值范围;
对一切x>0恒成立,求m的取值范围;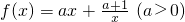 ,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.
,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.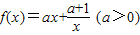 ,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.
,g(x)=4-x,已知满足f(x)=g(x)的x有且只有一个.