题目内容
已知x>0,观察下列几个不等式:x+
≥2;x+
≥3;x+
≥4;x+
≥5;…;归纳猜想一般的不等式为
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
| 256 |
| x4 |
x+
≥n+1,(n是正整数)
| nn |
| xn |
x+
≥n+1,(n是正整数)
.| nn |
| xn |
分析:根据题意,对给出的几个等式变形可得,x+
≥1+1,x+
≥2+1,x+
≥3+1,…,类推可得变化规律,左式为x+
,右式为n+1,即可得答案.
| 1 |
| x |
| 22 |
| x2 |
| 33 |
| x3 |
| nn |
| xn |
解答:解:根据题意,对给出的等式变形可得,x+
≥1+1,x+
≥2+1,x+
≥3+1,…,
则一般的不等式为x+
≥n+1,(n是正整数);
故答案为x+
≥n+1(n是正整数).
| 1 |
| x |
| 22 |
| x2 |
| 33 |
| x3 |
则一般的不等式为x+
| nn |
| xn |
故答案为x+
| nn |
| xn |
点评:本题考查归纳推理,解题的关键在于发现左式中
的变化规律.
| nn |
| xn |

练习册系列答案
相关题目
 ;
; ;
;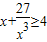 ;
;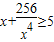 ;…;归纳猜想一般的不等式为 .
;…;归纳猜想一般的不等式为 .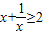 ;
; ;
; ;
;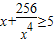 ;…;归纳猜想一般的不等式为 .
;…;归纳猜想一般的不等式为 . ;
; ;
;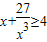 ;
; ;…;归纳猜想一般的不等式为 .
;…;归纳猜想一般的不等式为 .