题目内容
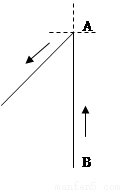
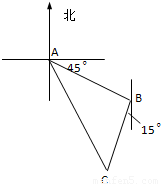
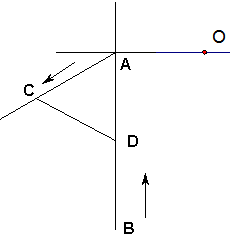 甲船在A处、乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以与乙船相同的速度由A处向南偏西60°方向行驶,如图所示,问经过多少小时后,甲、乙两船相距最近,此时两船相距多少海里?并请描述此时甲船相对与海岛O的位置.(海岛O在A的正东方向10海里处)
甲船在A处、乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以与乙船相同的速度由A处向南偏西60°方向行驶,如图所示,问经过多少小时后,甲、乙两船相距最近,此时两船相距多少海里?并请描述此时甲船相对与海岛O的位置.(海岛O在A的正东方向10海里处)分析:设经过x小时后,甲船和乙船分别到达C,D两点,表示出AC与AD,利用余弦定理列出关系式,利用二次函数的性质求出CD的最小值,以及此时x的值,根据三角形ACO为顶角为150°,底角为15°,腰长为10的等腰三角形,求出底边,即为AO的长.
解答:解:设经过x小时后,甲船和乙船分别到达C,D两点,
则AC=10x,AD=AB-BD=20-10x,
∴CD2=AC2+AD2-2AC•AD•cos60°=(10x)2+(20-10x)2-2×10x×(20-10x)×
=100x2+100x2-400x+400-200x+100x2=300x2-600x+400=300(x-1)2+100,
∵当CD2取得最小值100时,CD取得最小值10,
∴当x=1时,CD取得最小值,此时△ACD为等边三角形,
则经过1小时后,甲乙船相距最近,距离为10海里,
此时甲船在海岛O的西偏南15°处,与O相距2×10cos15°=5(
+
)(海里)(cos15°=cos(45°-30°)=
×
+
×
).
则AC=10x,AD=AB-BD=20-10x,
∴CD2=AC2+AD2-2AC•AD•cos60°=(10x)2+(20-10x)2-2×10x×(20-10x)×
| 1 |
| 2 |
∵当CD2取得最小值100时,CD取得最小值10,
∴当x=1时,CD取得最小值,此时△ACD为等边三角形,
则经过1小时后,甲乙船相距最近,距离为10海里,
此时甲船在海岛O的西偏南15°处,与O相距2×10cos15°=5(
| 6 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 4 |
点评:此题考查了正弦、余弦定理,二次函数的性质,以及等腰三角形的性质,熟练掌握定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
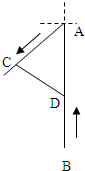 甲船在A处.乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以每小时8海里的速度由A处向南偏西60°方向行驶,问经过多少小时后,甲.乙两船相距最近?
甲船在A处.乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以每小时8海里的速度由A处向南偏西60°方向行驶,问经过多少小时后,甲.乙两船相距最近?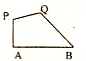 已知甲船在A处,乙船在甲船的正东方向10千米B处,现甲船以9千米/小时的速度沿正北方向航行,而乙船也以
已知甲船在A处,乙船在甲船的正东方向10千米B处,现甲船以9千米/小时的速度沿正北方向航行,而乙船也以