题目内容
设函数y=f(x)的定义域为R+,若对于给定的正数k,定义函数: ,则当函数
,则当函数 时,函数fk(x)的图象与直线
时,函数fk(x)的图象与直线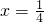 ,x=2,y=0围成的图形的面积为
,x=2,y=0围成的图形的面积为
- A.2ln2+2
- B.2ln2-1
- C.2ln2
- D.2ln2+1
D
分析:把k=1得入求得此分段函数的函数值并求出相应x的取值范围,然后利用定积分的几何意义,求出定积分的值即可.
解答:因为函数f(x)= ,K=1时,
,K=1时,
∴f1(x)= ?f1(x)=
?f1(x)=
∴函数fk(x)的图象与直线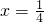 ,x=2,y=0围成的图形的面积为:
,x=2,y=0围成的图形的面积为:
 (x)dx=
(x)dx= +∫121dx=1+2ln2
+∫121dx=1+2ln2
故选D
点评:本小题主要考查分段函数、定积分的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:把k=1得入求得此分段函数的函数值并求出相应x的取值范围,然后利用定积分的几何意义,求出定积分的值即可.
解答:因为函数f(x)=
 ,K=1时,
,K=1时,∴f1(x)=
 ?f1(x)=
?f1(x)=
∴函数fk(x)的图象与直线
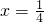 ,x=2,y=0围成的图形的面积为:
,x=2,y=0围成的图形的面积为: (x)dx=
(x)dx= +∫121dx=1+2ln2
+∫121dx=1+2ln2故选D
点评:本小题主要考查分段函数、定积分的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目