题目内容
已知函数f(x)= mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为 .
mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为 .
【答案】分析:函数f(x)= mx2+lnx-2x在定义域(x>0)内是增函数?
mx2+lnx-2x在定义域(x>0)内是增函数?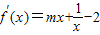 ≥0?
≥0?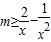 对于任意x>0.?
对于任意x>0.?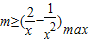 .利用导数即可得出.
.利用导数即可得出.
解答:解:∵函数f(x)= mx2+lnx-2x在定义域(x>0)内是增函数,∴
mx2+lnx-2x在定义域(x>0)内是增函数,∴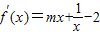 ≥0,化为
≥0,化为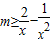 .
.
令g(x)=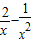 ,
,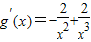 =-
=-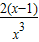 ,解g′(x)>0,得0<x<1;解g′(x)<0,得x>1.
,解g′(x)>0,得0<x<1;解g′(x)<0,得x>1.
因此当x=1时,g(x)取得最大值,g(1)=1.
∴m≥1.
故答案为[1,+∞).
点评:正确吧问题等价转化、利用导数研究函数的单调性、极值与最值是解题的关键.
 mx2+lnx-2x在定义域(x>0)内是增函数?
mx2+lnx-2x在定义域(x>0)内是增函数?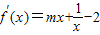 ≥0?
≥0?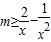 对于任意x>0.?
对于任意x>0.?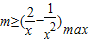 .利用导数即可得出.
.利用导数即可得出.解答:解:∵函数f(x)=
 mx2+lnx-2x在定义域(x>0)内是增函数,∴
mx2+lnx-2x在定义域(x>0)内是增函数,∴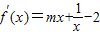 ≥0,化为
≥0,化为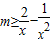 .
.令g(x)=
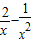 ,
,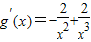 =-
=-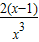 ,解g′(x)>0,得0<x<1;解g′(x)<0,得x>1.
,解g′(x)>0,得0<x<1;解g′(x)<0,得x>1.因此当x=1时,g(x)取得最大值,g(1)=1.
∴m≥1.
故答案为[1,+∞).
点评:正确吧问题等价转化、利用导数研究函数的单调性、极值与最值是解题的关键.

练习册系列答案
相关题目