题目内容
从直线x=1,y=1与两个坐标轴所围成的区域区内任意选一个点,这个点到原点的距离的平方大于1的概率是( )
分析:在坐标系中作出图形,可得满足条件的点位于正方形OABC内部,且在圆x2+y2=1的外部,即如图所示的阴影部分.再利用面积公式求出阴影部分面积,根据几何概型公式加以计算即可得到所求的概率.
解答:解:作出x=1、y=1与两个坐标轴所围成的图形,得到如图所示的正方形OABC .
.
∵到原点的距离的平方大于1的点,位于圆x2+y2=1的外部,
∴满足条件的点位于正方形OABC内部,且在圆x2+y2=1的外部,
即如图所示的阴影部分,
∵阴影部分面积为S阴影=S正方形-S扇形OAC=1-
,
∴所求概率为P=
=
=1-
,
故选:D
 .
.∵到原点的距离的平方大于1的点,位于圆x2+y2=1的外部,
∴满足条件的点位于正方形OABC内部,且在圆x2+y2=1的外部,
即如图所示的阴影部分,
∵阴影部分面积为S阴影=S正方形-S扇形OAC=1-
| π |
| 4 |
∴所求概率为P=
| S阴影 |
| S正方形 |
1-
| ||
| 1 |
| π |
| 4 |
故选:D
点评:本题给出坐标平面内的区域,求选取的点满足条件的概率.着重考查了正方形、扇形面积公式和几何概型的计算等知识,属于基础题.

练习册系列答案
相关题目
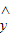 =
=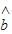 x+
x+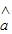 一定经过其样本数据点 (x1,y1),(x2,y2),…,(xn,yn)中的一个点;
一定经过其样本数据点 (x1,y1),(x2,y2),…,(xn,yn)中的一个点;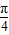 ;
;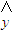 =
=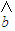 x+
x+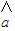 一定经过其样本数据点 (x1,y1),(x2,y2),…,(xn,yn)中的一个点;
一定经过其样本数据点 (x1,y1),(x2,y2),…,(xn,yn)中的一个点;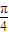 ;
;