题目内容
已知f(x)=
在点x=3处连续，则常数a的值为（ ）
|
| A、-1 | B、3 | C、5 | D、2 |
分析：当x＜3时，f(x)=
=x+3，又f（3）=a+log33=a+1，若要f（x）在x=3处连续，则应使得3+3=a+1，即：a=5．
| x2-9 |
| x-3 |
解答：解：f（3）=a+log33=a+1，当x＜3时，f(x)=
=x+3，因为f（x）在x=3处连续，则3+3=a+1，解得：a=5．故选C．
| x2-9 |
| x-3 |
点评：考查分段函数的连续性，要想分段函数在分段点处连续，则必须满足两个解析式在该点处的值相等．对于该题有很多同学会提出“怎么能够把x=3代入f(x)=
=x+3=3+3里面呢？不是没有定义吗？”这样的疑问．f(x)=
=x+3（x＞3）确实在x=3处没有定义，但是假如有定义就可以求出一个值，这个值必须等于f（3），这样才能使得f（x）在x=3处连续．
| x2-9 |
| x-3 |
| x2-9 |
| x-3 |
练习册系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
R)，l(x)= 2x2+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求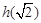
；
，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；
R)，
=
2x2+3x-1，h (x)为f
(x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求
；
，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；