题目内容
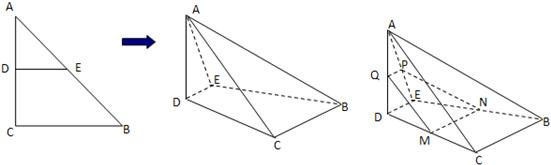
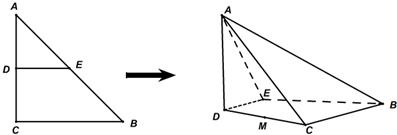 如图,沿等腰直角三角形ABC的中位线DE,将平面ADE折起,使得平面ADE⊥平面BCDE得到四棱锥A-BCDE.
如图,沿等腰直角三角形ABC的中位线DE,将平面ADE折起,使得平面ADE⊥平面BCDE得到四棱锥A-BCDE.(1)求证:平面ABC⊥平面ACD;
(2)过CD的中点M的平面α与平面ABC平行,试求平面α与四棱锥A-BCDE各个面的交线所围成多边形的面积与三角形ABC的面积之比.
分析:(1)AD⊥DE,平面ADE⊥平面BCDE,根据两个平面垂直的性质定理得AD⊥平面BCDE,所以AD⊥BC,又CD⊥BC,根据线面垂直的判定定理BC⊥平面ACD,BC?平面ABC,所以平面ABC⊥平面ACD
(2)由于平面α∥平面ABC,故平面ACD与平面α的交线MQ∥AC,M是CD的中点,故Q是AD的中点;同理平面BCDE与平面α的交线MN∥BC,N为BE的中点;平面ABE的交线NP∥AB,P为AE的中点,连接PQ即为平面α与平面ADE的交线,故平面α与四棱锥A-BCDE各个面的交线所围成多边形就是四边形MNPQ,进一步观察可知四边形MNPQ是直角梯形,进而由比例关系可以求得截面面积与△ABC的面积之比
(2)由于平面α∥平面ABC,故平面ACD与平面α的交线MQ∥AC,M是CD的中点,故Q是AD的中点;同理平面BCDE与平面α的交线MN∥BC,N为BE的中点;平面ABE的交线NP∥AB,P为AE的中点,连接PQ即为平面α与平面ADE的交线,故平面α与四棱锥A-BCDE各个面的交线所围成多边形就是四边形MNPQ,进一步观察可知四边形MNPQ是直角梯形,进而由比例关系可以求得截面面积与△ABC的面积之比
解答: 解:(1)∵AD⊥DE,平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
解:(1)∵AD⊥DE,平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
∴AD⊥平面BCDE,
∴AD⊥BC,
又∵CD⊥BC,AD∩CD=D,
∴BC⊥平面ACD,
又∵BC?平面ABC,
∴平面ABC⊥平面ACD
(2)∵平面α∥平面ABC,设平面ACD与平面α的交线为MQ,
∴MQ∥AC,
又∵M是CD的中点,
∴Q是AD的中点;
同理:设平面BCDE与平面α的交线为MN,
∴MN∥BC,
又∵M是CD的中点,
∴N为BE的中点;
同理:平面ABE的交线NP∥AB,P为AE的中点,
连接PQ即为平面α与平面ADE的交线,故平面α与四棱锥A-BCDE各个面的交线所围成多边形是图中的四边形MNPQ,
由于PQ∥DE,DE∥MN,故PQ∥MN,根据(1)BC⊥AC,由MN∥BC,MQ∥AC,故MQ⊥MN,即四边形MNPQ′是直角梯形.
设CM=a,则MQ=
a,MN=3a,PQ=a,BC=4a,AC=2
a,故四边形MNPQ的面积是
×
a=2
a2,三角形ABC的面积是
×4a×2
a=4
a2,
故平面α与四棱锥A-BCDE各个面的交线所围成多边形的面积与三角形ABC的面积之比为
=
.
 解:(1)∵AD⊥DE,平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
解:(1)∵AD⊥DE,平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,∴AD⊥平面BCDE,
∴AD⊥BC,
又∵CD⊥BC,AD∩CD=D,
∴BC⊥平面ACD,
又∵BC?平面ABC,
∴平面ABC⊥平面ACD
(2)∵平面α∥平面ABC,设平面ACD与平面α的交线为MQ,
∴MQ∥AC,
又∵M是CD的中点,
∴Q是AD的中点;
同理:设平面BCDE与平面α的交线为MN,
∴MN∥BC,
又∵M是CD的中点,
∴N为BE的中点;
同理:平面ABE的交线NP∥AB,P为AE的中点,
连接PQ即为平面α与平面ADE的交线,故平面α与四棱锥A-BCDE各个面的交线所围成多边形是图中的四边形MNPQ,
由于PQ∥DE,DE∥MN,故PQ∥MN,根据(1)BC⊥AC,由MN∥BC,MQ∥AC,故MQ⊥MN,即四边形MNPQ′是直角梯形.
设CM=a,则MQ=
| 2 |
| 2 |
| a+3a |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故平面α与四棱锥A-BCDE各个面的交线所围成多边形的面积与三角形ABC的面积之比为
2
| ||
4
|
| 1 |
| 2 |
点评:本小题主要考查空间线面关系、多边形的面积计算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目