题目内容
单调函数f(x)满足f(ax+3)=x,其中a＞0,若f-1(x)的定义域为［-
，
］. (Ⅰ)求f(x)的解析式和定义域D；
(Ⅱ)当b∈D时，求关于x的方程
=|b-1|+1的根的取值范围.
解：(Ⅰ)令ax+3=t，则ax=t-3，x=t-,
∴f(t)=t-
,即f(x)=
x-
，
由于a＞0,∴f(x)为增函数.
由于f-1(x)的定义域为［-
,
］,
∴f(x)的值域为［-
,
］.
令
≤
x-
≤
,
解得-4≤x≤6.
因此f(x)的定义域为：D=［-4,6］.
(Ⅱ)当b=-4时，方程
=|b-1|+1无解，因此b≠-4,这时，x=(b+4)［|b-1|+1］=
当-4＜b≤1时，x∈(0,9);当1＜b≤6时，x∈(5,60],
综上所述，该方程的根的取值范围是(0,60］.
练习册系列答案
相关题目
3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．
)+f(3
)+f(3
)+f(3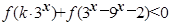
，对任意x∈R恒成立，求实数k的取值范围
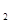3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．(1)求证f(x)为奇函数；(2)若f(k·3
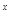)+f(3