题目内容
(1)求证: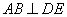 ;
;
(2)求直线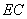 与平面
与平面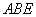 所成角的正弦值;
所成角的正弦值;
(3)线段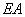 上是否存在点
上是否存在点 ,使
,使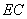 // 平面
// 平面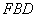 ?若存在,求
?若存在,求
出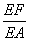 ;若不存在,说明理由.
;若不存在,说明理由.

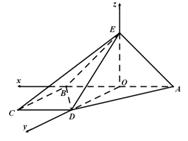 因为四边形
因为四边形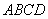 为直角梯形,
为直角梯形,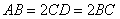 ,
,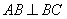 ,
,
所以四边形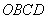 为正方形,所以
为正方形,所以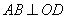 .
.
所以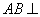 平面
平面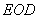 . 所以
. 所以 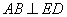 .……4分
.……4分
解:(Ⅱ)因为平面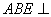 平面
平面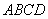 ,且
,且 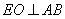 ,
,
所以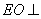 平面
平面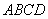 ,所以
,所以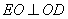 . 由
. 由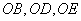 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系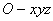 .因为三角形
.因为三角形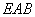 为等腰直角三角形,所以
为等腰直角三角形,所以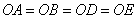 ,设
,设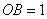 ,所以
,所以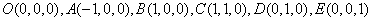 . 所以
. 所以 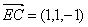 ,平面
,平面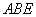 的一个法向量为
的一个法向量为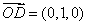 . 设直线
. 设直线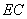 与平面
与平面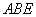 所成的角为
所成的角为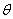 ,所以
,所以 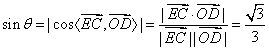 , 即直线
, 即直线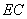 与平面
与平面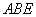 所成角的正弦值为
所成角的正弦值为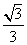 .…8分
.…8分
(Ⅲ)存在点 ,且
,且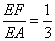 时,有
时,有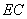 // 平面
// 平面 . 证明如下:由
. 证明如下:由 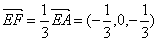 ,
,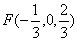 ,所以
,所以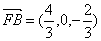 .
.
设平面 的法向量为
的法向量为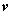
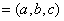 ,则有
,则有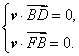 所以
所以 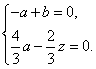 取
取 ,得
,得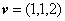 .因为
.因为 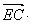
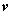
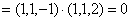 ,且
,且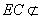 平面
平面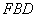 ,所以
,所以 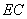 // 平面
// 平面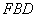 . 即点
. 即点 满足
满足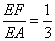 时,有
时,有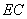 // 平面
// 平面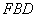 .…………12分
.…………12分

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,点A的极坐标为A(
,点A的极坐标为A( ),则点A到直线l的距离为 .
),则点A到直线l的距离为 .
 与曲线
与曲线 只有一个公共点,求
只有一个公共点,求 的取值范围;
的取值范围; 时,求曲线
时,求曲线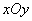 中,直线
中,直线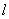 的方程为
的方程为 ,曲线
,曲线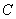 的参数方程为
的参数方程为 (
( 为参数).
为参数).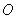 为极点,以
为极点,以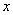 轴正半轴为极轴)中,点P的极坐标为
轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线
 ,不等式
,不等式 恒成立,则实数a的取值范围是________.
恒成立,则实数a的取值范围是________.