题目内容
若定义在区间D上的函数f(x)对于D上的任意n个值x1,x2,…,xn总满足,| f(x1)+f(x2)+…+f(xn) |
| n |
| x1+x2+x3+…+xn |
| n |
| π |
| 2 |
分析:利用已知结论,可将cosA+cosB+cosC转化为A+B+C的余弦求解,因为A+B+C=180°为定值,即可得到结论.
解答:解:利用已知结论,则cosA+cosB+cosC≤3cos(
)=3cos
=
,
故答案为:
| A+B+C |
| 3 |
| π |
| 3 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查演绎推理、考查对式子的观察和运用能力、利用已知结论解决问题的能力.

练习册系列答案
相关题目

 的单调性;
的单调性;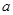 的取值范围;
的取值范围;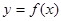 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式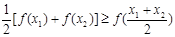 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数 ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.