题目内容
函数f(x)=
- A.在[0,
 ),(
),( ,π]上递增,在[π,
,π]上递增,在[π, ),(
),( ,2π]上递减
,2π]上递减 - B.在[0,
 ),[π,
),[π, )上递增,在(
)上递增,在( ,π],(
,π],( ,2π]上递减
,2π]上递减 - C.在(
 ,π],(
,π],( ,2π]上递增,在[0,
,2π]上递增,在[0, ),[π,
),[π, )上递减
)上递减 - D.在[π,
 ),(
),( ,2π]上递增,在[0,
,2π]上递增,在[0, ),(
),( ,π]上递减
,π]上递减
A
分析:先化简函数解析式,再根据正切函数的单调性可解题.
解答:∵f(x)= =
=
当sinx>0时,即x∈[0.π]时f(x)=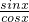 =tanx(x≠
=tanx(x≠ )
)
当sinx<0时,即x∈[π,2π]时f(x)= =-tanx(x≠
=-tanx(x≠ )
)
根据正切函数的单调性可知:函数f(x)在[0, ),(
),( ,π]上递增,在[π,
,π]上递增,在[π, ),(
),( ,2π]上递减
,2π]上递减
故选A.
点评:本题主要考查正切函数的单调性.一定要注意正切函数的定义域即{x|x≠ ,k∈Z}.
,k∈Z}.
分析:先化简函数解析式,再根据正切函数的单调性可解题.
解答:∵f(x)=
 =
=
当sinx>0时,即x∈[0.π]时f(x)=
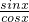 =tanx(x≠
=tanx(x≠ )
)当sinx<0时,即x∈[π,2π]时f(x)=
 =-tanx(x≠
=-tanx(x≠ )
)根据正切函数的单调性可知:函数f(x)在[0,
 ),(
),( ,π]上递增,在[π,
,π]上递增,在[π, ),(
),( ,2π]上递减
,2π]上递减故选A.
点评:本题主要考查正切函数的单调性.一定要注意正切函数的定义域即{x|x≠
 ,k∈Z}.
,k∈Z}. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在R上是奇函数.
在R上是奇函数. 在R上的奇函数。
在R上的奇函数。 在R上是奇函数.
在R上是奇函数.