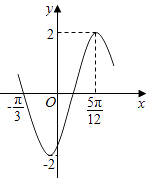题目内容
【题目】已知函数f(x)= ![]() cosx(sinx+cosx). (Ⅰ)若0<α<
cosx(sinx+cosx). (Ⅰ)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
【答案】解:(Ⅰ)∵0<α< ![]() ,且sinα=
,且sinα= ![]() , ∴cosα=
, ∴cosα= ![]() ,
,
∴f(α)= ![]() cosα(sinα+cosα)
cosα(sinα+cosα)
= ![]() ×
× ![]() ×(
×( ![]() +
+ ![]() )
)
= ![]() ;
;
(Ⅱ)函数f(x)= ![]() cosx(sinx+cosx)
cosx(sinx+cosx)
= ![]() (cosxsinx+cos2x)
(cosxsinx+cos2x)
= ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]() ,
,
∴f(x)的最小正周期为π;
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴函数f(x)的单调减区间为[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
【解析】(Ⅰ)根据同角的三角函数关系,求出sinα、cosα的值,再计算f(α)的值;(Ⅱ)化函数f(x)为正弦型函数,即可求出f(x)的最小正周期和单调减区间.

练习册系列答案
相关题目