题目内容
19.已知矩阵$A=[\begin{array}{l}2\\ 1\end{array}\right.$$\left.\begin{array}{l}1\\ 3\end{array}]$,$B=[\begin{array}{l}1\\ 0\end{array}\right.$$\left.\begin{array}{l}1\\-1\end{array}]$.求矩阵C,使得AC=B.分析 求出A-1,由AC=B,得(A-1A)C=A-1B,即可得出结论.
解答 解:因为|A|=2×3-1×1=5,
所以${A^{-1}}=[{\begin{array}{l}{\frac{3}{5}}&{-\frac{1}{5}}\\{-\frac{1}{5}}&{\frac{2}{5}}\end{array}}]=[{\begin{array}{l}{\frac{3}{5}}&{-\frac{1}{5}}\\{-\frac{1}{5}}&{\frac{2}{5}}\end{array}}]$,
由AC=B,得(A-1A)C=A-1B,
所以$C={A^{-1}}B=[{\begin{array}{l}{\frac{3}{5}}&{-\frac{1}{5}}\\{-\frac{1}{5}}&{\frac{2}{5}}\end{array}}][{\begin{array}{l}1&1\\ 0&{-1}\end{array}}]=[{\begin{array}{l}{\frac{3}{5}}&{\frac{4}{5}}\\{-\frac{1}{5}}&{-\frac{3}{5}}\end{array}}]$.
点评 本题考查矩阵的乘法,考查逆矩阵的求法,考查学生的计算能力,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.已知集合A={-2,-1,0,1,2},B={x|lgx≤0},则A∩B=( )
| A. | {1} | B. | {0,1} | C. | {0,1,2} | D. | {1,2} |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,以F1F2为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
11.已知一个半径为$\sqrt{7}$的球中有一个各条棱长都相等的内接正三棱柱,则这正三棱柱的体积是( )
| A. | 18 | B. | 16 | C. | 12 | D. | 8 |
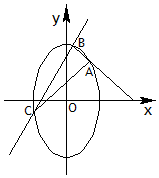 如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.
如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.