题目内容
已知曲线 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线
,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线 的参数方程
的参数方程
(Ⅰ)写出直线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线 ,在曲线
,在曲线 上求一点
上求一点 ,使点
,使点 到直线
到直线 的距离最小,并求出最小距离.
的距离最小,并求出最小距离.
【答案】
(1) ,
,
(2)
【解析】
试题分析:.解:(Ⅰ)由 得,
得, ,
,
由 得,圆
得,圆 .
.
(Ⅱ)设点 是圆C上的任意一点,经过伸缩变换
是圆C上的任意一点,经过伸缩变换 得到点
得到点
由 得
得 ,把
,把 代入圆
代入圆 得,
得,
所以曲线
令 ,则点
,则点 到直线
到直线 的距离
的距离


∴当 即
即 时,
时, ,此时,
,此时,
∴当 时,点
时,点 到直线
到直线 的距离的最小值为
的距离的最小值为 .
.
考点:点到直线的距离,参数方程与直角坐标方程
点评:主要是考查了参数方程与直角坐标方程的互化,以及点到直线的距离公式的求解,属于中档题。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知曲线的极坐标方程为ρ=4cos2
-2,则其直角坐标下的方程是( )
| θ |
| 2 |
| A、x2+(y+1)2=1 |
| B、(x+1)2+y2=1 |
| C、(x-1)2+y2=1 |
| D、x2+(y-1)2=1 |
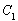
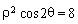
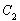
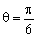
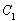
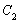
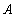
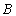
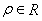
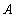
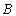
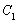

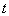
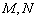
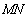
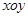 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线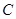 的极坐标方程为
的极坐标方程为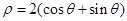 .
.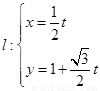 (
(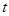 为参数)与曲线C交于
为参数)与曲线C交于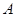 ,
,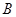 两点,与
两点,与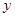 轴交于
轴交于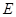 ,求
,求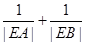 的值.
的值. 的极坐标方程是
的极坐标方程是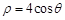 ,以极点为原点,极轴为
,以极点为原点,极轴为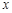 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: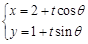 (为参数).
(为参数).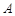 ,
,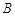 两点,点
两点,点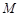 的直角坐标为
的直角坐标为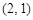 ,若
,若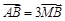 ,求直线的普通方程.
,求直线的普通方程.