题目内容
18．已知圆C过点O（0，0），和点T（1，3），且圆心在直线n：x-2y=0上，直线l：x+my-2m-1=0，m∈R，（1）若直线n与直线l平行，求这两条平行线间的距离；
（2）求圆C的方程；
（3）设直线l恒过定点A，求点A的坐标并判断点A与圆C的位置关系．
分析 （1）求出m，利用两条平行线间的距离公式，求这两条平行线间的距离；
（2）设圆心坐标为（2a，a），利用两点间的距离公式，建立方程，求出圆心与半径，即可求圆C的方程；
（3）直线l：x+my-2m-1=0，即m（y-2）+（x-1）=0，可得直线l恒过定点A的坐标，再判断点A与圆C的位置关系．
解答 解：（1）由题意，m=-2，直线l：x-2y+3=0，
∴两条平行线间的距离d=$\frac{3}{\sqrt{1+4}}$=$\frac{3\sqrt{5}}{5}$；
（2）设圆心坐标为（2a，a），
则4a2+a2=（2a-1）2+（a-3）2，∴a=1，r=$\sqrt{5}$，
∴圆C的方程（x-2）2+（y-1）2=5；
（3）直线l：x+my-2m-1=0，即m（y-2）+（x-1）=0，∴直线l恒过定点A（1，2），
∵（1-2）2+（2-1）2＜5，
∴A在圆C的内部．
点评 本题考查直线与圆的方程，考查直线过定点，考查学生的计算能力，属于中档题．
练习册系列答案
巧学巧练系列答案
相关题目
8．已知某离散型随机变量X的分布列如表格，则m=$\frac{7}{12}$．
| X | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m |
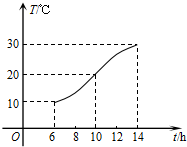某地一天中6时至14时的温度变化曲线近似满足函数T=Asin（ωt+φ）+b（其中$\frac{π}{2}$＜φ＜π），6时至14时期间的温度变化曲线如图所示，它是上述函数的半个周期的图象，那么这一天6时至14时温差的最大值是20°C；图中曲线对应的函数解析式是y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20，x∈[6，14]．
3．已知命题p：?x∈R，使得x2-x+2＜0；命题函数f（x）=$\frac{4}{x}$-log3x在区间（3，4）内没有零点．下列命题为真命题的是（ ）
| A． | （￢p）∧（￢q） | B． | p∧q | C． | （￢p）∧p） | D． | （p）∨q |