题目内容
设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.(I)求点C的轨迹E的方程;
(II)若l是过点P(1,0)且垂直于x轴的直线,是否存在直线l,使得l与曲线E交于两个不同的点M,N,且MN恰被l平分?若存在,求出l的斜率的取值范围;若不存在,请说明理由.

【答案】分析:(I)设C(x,y),由重心坐标公式的到G的坐标,再由GQ∥AB及Q在x轴上得到Q的坐标,又由|QB|=|QC建立方程.
(II)假设存在直线l:y=kx+m,代入迹E的方程,利用判别式大于0,及交点的中点横坐标为1,解出斜率的范围.
解答:解:(I)设C(x,y),则 ,因为GQ∥AB,可得
,因为GQ∥AB,可得 ;又由|QB|=|QC|,
;又由|QB|=|QC|,
可得点C的轨迹E的方程为 .(6分)(没有x≠0扣1分)
.(6分)(没有x≠0扣1分)
(II)假设存在直线l:y=kx+m,代入
并整理得(1+3k2)x2+6mkx+3(m2-1)=0,(8分)
设M(x1,y1),N(x2,y2),
则 (*)(10分)
(*)(10分)
又△=36m2k2-12(1+3k2)(m2-1)
= =
= ,
,
解得 或
或 (13分)
(13分)
特别地,若m=±1,代入(*)得,3k2±3k+1=0,此方程无解,即x≠0.
综上,l的斜率的取值范围是 或
或 .(14分)
.(14分)
点评:本题考查轨迹方程的求法,直线和圆锥曲线的位置关系.
(II)假设存在直线l:y=kx+m,代入迹E的方程,利用判别式大于0,及交点的中点横坐标为1,解出斜率的范围.
解答:解:(I)设C(x,y),则
 ,因为GQ∥AB,可得
,因为GQ∥AB,可得 ;又由|QB|=|QC|,
;又由|QB|=|QC|,可得点C的轨迹E的方程为
 .(6分)(没有x≠0扣1分)
.(6分)(没有x≠0扣1分)(II)假设存在直线l:y=kx+m,代入

并整理得(1+3k2)x2+6mkx+3(m2-1)=0,(8分)
设M(x1,y1),N(x2,y2),
则
 (*)(10分)
(*)(10分)又△=36m2k2-12(1+3k2)(m2-1)
=
 =
= ,
,解得
 或
或 (13分)
(13分)特别地,若m=±1,代入(*)得,3k2±3k+1=0,此方程无解,即x≠0.
综上,l的斜率的取值范围是
 或
或 .(14分)
.(14分)点评:本题考查轨迹方程的求法,直线和圆锥曲线的位置关系.

练习册系列答案
相关题目
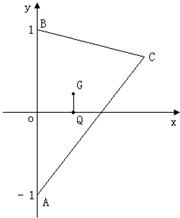 设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.
设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.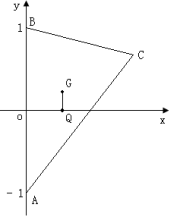
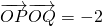 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.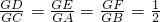 .
.