题目内容
(本小题满分13分)设数列 是首项为
是首项为 ,公差为
,公差为 的等差数列,且
的等差数列,且 是等比数列
是等比数列 的前三项.
的前三项.
(1)求 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1)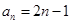 ;(2)
;(2) .
.
解析试题分析:(1)由等差数列的通项公式可知,  .又因为
.又因为 成等比,则有
成等比,则有 ,即
,即 .则可得
.则可得 或
或 .当
.当 时,
时,  与等比数列相矛盾,故舍.然后可有等差数列的通项公式求其通项.(2)由(1)可得数列
与等比数列相矛盾,故舍.然后可有等差数列的通项公式求其通项.(2)由(1)可得数列 的前三项,根据等比数列的前
的前三项,根据等比数列的前 项和公式可得
项和公式可得 .
.
试题解析:解:(1)由题意可知: . 2分
. 2分
因为  成等比数列,
成等比数列,
所以  . 4分
. 4分
因为  ,
,
所以  .
.
若 ,则
,则 ,与
,与 成等比数列矛盾.
成等比数列矛盾.
所以 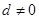 .
.
所以  . 7分
. 7分
所以  . 9分
. 9分
(2)因为  ,
, , 11分
, 11分
所以 等比数列 的首项为
的首项为 ,公比为
,公比为 .
.
所以  . 13分
. 13分
考点:1等差数列的通项公式;2等比数列的前 项和.
项和.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
一个算法的程序框图如图所示,则该程序运行后输出的值是( ).
| A.4 | B.5 | C.6 | D.7 |
已知直线 与直线
与直线 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
| A.1 | B.2 | C. | D.4 |
如果输入 ,那么执行下图中算法后的输出结果是( )
,那么执行下图中算法后的输出结果是( )
A. | B. | C. | D. |
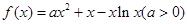 .
.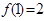 ,且在定义域内
,且在定义域内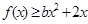 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;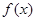 在定义域上是单调函数,求实数a的取值范围;
在定义域上是单调函数,求实数a的取值范围; 时,试比较
时,试比较 与
与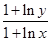 的大小.
的大小. 与
与 的夹角为
的夹角为 ,若(
,若( )
) (
( ),则
),则 .
.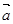
 ,向量
,向量 ,则
,则 方向上的投影为____.
方向上的投影为____. ,对于任意自然数
,对于任意自然数 都是递增数列,
都是递增数列, 的取值范围为 .
的取值范围为 . ,则关于x的不等式f(x2)>f(3-2x)的解集是_______________.
,则关于x的不等式f(x2)>f(3-2x)的解集是_______________.