题目内容
有一块形状为直角梯形材料ABCD，其尺寸如图所示（单位：分米），现从中截取一块矩形材料EBFP，点P在CD上，设FP=x（1）用x表示EP的长度l
（2）设矩形EBFP的面积为y，求y关于X的函数解析式
（3）当x为何值时，矩形EBFP的面积最大，最大面积为多少？
分析：（1）从D垂直往下，交BC与点M，PF∥DM，根据
=
可求出CF，从而求出EP；
（2）直接利用矩形的面积公式，矩形的面积=长×宽进行求解即可；
（3）根据开口向下二次函数在对称轴处取最大值，从而求出所求．
| PF |
| DM |
| CF |
| CM |
（2）直接利用矩形的面积公式，矩形的面积=长×宽进行求解即可；
（3）根据开口向下二次函数在对称轴处取最大值，从而求出所求．
解答：解：（1）加一条辅助线从D垂直往下，交BC与点M，
PF∥DM，则
=
即
=
解得FC=
∴EP=5-
（2）设矩形EBFP的面积为y，
则y=（5-
）x x∈（0，3）
（3）y=（5-
）x x∈（0，3）
=5x-
开口向下的二次函数在对称轴x=
时取最大面积
PF∥DM，则
| PF |
| DM |
| CF |
| CM |
| x |
| 3 |
| FC |
| 4 |
解得FC=
| 4x |
| 3 |
∴EP=5-
| 4x |
| 3 |
（2）设矩形EBFP的面积为y，
则y=（5-
| 4x |
| 3 |
（3）y=（5-
| 4x |
| 3 |
=5x-
| 4x2 |
| 3 |
开口向下的二次函数在对称轴x=
| 15 |
| 8 |
| 75 |
| 16 |
点评：本题主要考查了三角形相似，以及二次函数求最值，考查了函数模型的选择与应用，属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
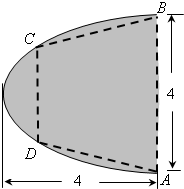
如图，有一块抛物线形状的钢板，计划将此钢板切割成等腰梯形ABCD的形状，使得A，B，C，D都落在抛物线上，点A，B关于抛物线的对称轴对称且AB=4，抛物线的顶点到底边AB的距离是4，记CD=2t，梯形面积为S．以抛物线的顶点为坐标原点，其对称轴为x轴，建立平面直角坐标系．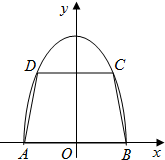
如图，有一块半椭圆形钢板，其长半轴长为2r，短半轴长为r，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S．以AB为x轴，AB中点为原点建立平面直角坐标系．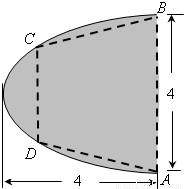
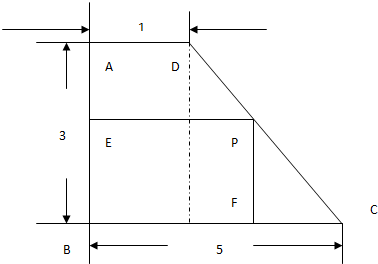有一块形状为直角梯形材料ABCD，其尺寸如图所示（单位：分米），现从中截取一块矩形材料EBFP，点P在CD上，设FP=x