题目内容
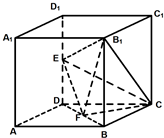 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.(1)求证:EF∥平面ABC1D1;
(2)求证:EF⊥B1C;
(3)求三棱锥VB1-EFC的体积.
分析:(1)欲证EF∥平面ABC1D1,根据直线与平面平行的判定定理可知只需证EF与平面ABC1D1内一直线平行,连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,根据中位线定理可知EF∥D1B,满足定理所需条件;
(2)先根据线面垂直的判定定理证出B1C⊥平面ABC1D1,而BD1?平面ABC1D1,根据线面垂直的性质可知B1C⊥BD1,而EF∥BD1,根据平行的性质可得结论;
(3)可先证CF⊥平面EFB1,根据勾股定理可知∠EFB1=90°,根据等体积法可知VB1-EFC=V C-B1EF,即可求出所求.
(2)先根据线面垂直的判定定理证出B1C⊥平面ABC1D1,而BD1?平面ABC1D1,根据线面垂直的性质可知B1C⊥BD1,而EF∥BD1,根据平行的性质可得结论;
(3)可先证CF⊥平面EFB1,根据勾股定理可知∠EFB1=90°,根据等体积法可知VB1-EFC=V C-B1EF,即可求出所求.
解答:解:(1)证明:连接BD1,如图,在△DD1B中,E、F分别为D1D,DB的中点,则
?EF∥平面ABC1D1.
(2)
?
?
?EF⊥B1C
(3)∵CF⊥平面BDD1B1,∴CF⊥平面EFB1且CF=BF=
,
∵EF=
BD1=
,B1F=
=
=
,
B1E=
=
=3
∴EF2+B1F2=B1E2即∠EFB1=90°,
∴VB1-EFC=VC-B1EF=
•S△B1EF•CF
=
×
•EF•B1F•CF=
×
×
×
×
=1
|
(2)
|
|
|
(3)∵CF⊥平面BDD1B1,∴CF⊥平面EFB1且CF=BF=
| 2 |
∵EF=
| 1 |
| 2 |
| 3 |
| BF2+BB12 |
(
|
| 6 |
B1E=
| B1D12+D1E2 |
12+(2
|
∴EF2+B1F2=B1E2即∠EFB1=90°,
∴VB1-EFC=VC-B1EF=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 6 |
| 2 |
点评:本题主要考查了线面平行的判定,以及线面垂直的性质和三棱锥体积的计算,同时考查了空间想象能力、运算求解能力、转化与划归的思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
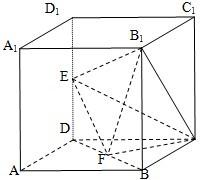 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.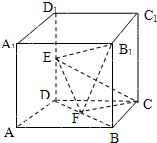 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点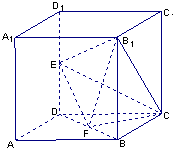 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 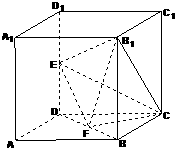 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.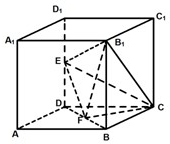 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.