题目内容
若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值范围为( )A.(0,1)
B.(0,1]
C.(-∞,1)
D.(-∞,1]
【答案】分析:求出圆心坐标代入直线方程得到m,n的关系m+n=2;将,利用基本不等式mn≤ 求出结果.
求出结果.
解答:解:因为直线平分圆,所以直线过圆心
圆心坐标为(2,1)
∴m+n=2
∴mn≤ =1(当且仅当m=n时,取等号)
=1(当且仅当m=n时,取等号)
∴mn的取值范围为(-∞,1]
故选D.
点评:本题考查直线平分圆时直线过圆心、考查利用基本不等式求函数的最值需注意:一正、二定、三相等.
 求出结果.
求出结果.解答:解:因为直线平分圆,所以直线过圆心
圆心坐标为(2,1)
∴m+n=2
∴mn≤
 =1(当且仅当m=n时,取等号)
=1(当且仅当m=n时,取等号)∴mn的取值范围为(-∞,1]
故选D.
点评:本题考查直线平分圆时直线过圆心、考查利用基本不等式求函数的最值需注意:一正、二定、三相等.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值范围为( )
| A、(0,1) | B、(0,1] | C、(-∞,1) | D、(-∞,1] |
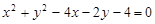 的周长,则mn的取值范围是( )
的周长,则mn的取值范围是( )