题目内容
(本小题12分)已知函数
，若函数
与
的图象的一个交点
的横坐标为1，且两曲线在点处的切线互相垂直.
⑴求：函数
的单调递增区间.
⑵若对任意
，不等式
恒成立，求：实数
的取值范围.
解：⑴由题意：
，
……①
又
，
的图象在点
切线的斜率为：
又
,
的图象在点切线的斜率为：
……………②
由①②可解得：
，
，………………………… 3分
，
令
，解得：
即函数
的单调递增区间为：
．………………………………… 6分
⑵对任意
，
恒成立
当时，
成立………(★) ………………………… 8分
，令
，解得：
区间
上递减，在区间
上递增
又
，当
时，
……… 10分
而
，
当时，
由(★)式有：
，实数
的取值范围为：
．……… 12分
练习册系列答案
相关题目
，
，直线
与函数
、
的k*s#5^u图象都相切，且与函数
.
的k*s#5^u值；
(其中
是
的k*s#5^u最大值；
时，求证：
.
中，
。
中，
，求数列
项和
.
轴上的抛物线与直线
交于P、Q两点，|PQ|=
，求抛物线的方程
；
过
且与圆C相切，求直线
，使直线
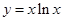
处的切线方程。