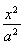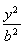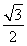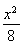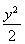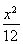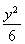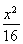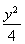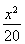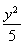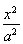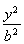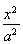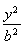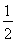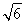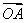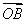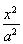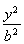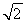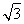题目内容
已知椭圆C:
思路分析:由题意Q(x,y),使∠AQB=120°成立,且-a≤x≤a,-b≤y≤b,若x、y用a、b、c表示,则出现了a、b、c的不等关系,从而求e的范围.
解:A(-a,0)、B(a,0),设Q(x,y).由椭圆的对称性,不妨设Q点在x轴的上方,即y>0,∴kAQ=![]() ,kBQ=
,kBQ=![]() .由tan∠AQB=tan120°=-
.由tan∠AQB=tan120°=-![]() ,依到角公式得
,依到角公式得
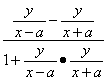 =-
=-![]() ,即
,即![]() (x2+y2-a2)=-2ay. ①
(x2+y2-a2)=-2ay. ①
又Q在椭圆C上,
故![]() =1. ②
=1. ②
由①②消去x,得![]() (b2-a2)y2+2ab2y=0,而y≠0,
(b2-a2)y2+2ab2y=0,而y≠0,
∴y=![]() .
.
又y≤b,
∴![]() ≤b,即
≤b,即![]() ≤1.
≤1.
∴4a2b2≤3c4,即4a2(a2-c2)≤3c4.
∴3e4+4e2-4≥0,解得e2≥![]() .
.
∴![]() ≤e<1.
≤e<1.
温馨提示
这里借助于x、y与a、b、c的关系,表示出关于a、b、c的一个不等关系式是关键所在,在求离心率范围的问题中常用这种思路.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目