题目内容
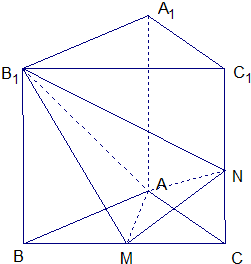 如图,在直三棱柱ABC-A1B1C1中,AA1=2,AB=AC=1,∠BAC=90°,点M是BC的中点,点N在侧棱CC1上.
如图,在直三棱柱ABC-A1B1C1中,AA1=2,AB=AC=1,∠BAC=90°,点M是BC的中点,点N在侧棱CC1上.(1)当线段CN的长度为多少时,NM⊥AB1;
(2)若MN⊥AB1,求异面直线B1N与AB所成的角的正切值;
(3)若MN⊥AB1,求二面角A-B1N-M的大小
(4)若MN⊥AB1,求点M到平面AB1N的距离.
分析:(1)先根据条件得到MN⊥面AB1M,再结合B1C12+NC12=B1M2+NM2即可求出结论.
(2)AB平行于A1B1,∠A1BN就是异面直线所成的角,转化为求∠A1BN
(3)作ME⊥B1N,交B1N于E可得∠AEM为二面角A--B1N-M的平面角;计算出tan∠AEM即可.
(4)作MH⊥AE于H,根据条件得到MH的长即为点M到平面AB1N的距离,然后在直角三角形AME中,求出MH即可.
(2)AB平行于A1B1,∠A1BN就是异面直线所成的角,转化为求∠A1BN
(3)作ME⊥B1N,交B1N于E可得∠AEM为二面角A--B1N-M的平面角;计算出tan∠AEM即可.
(4)作MH⊥AE于H,根据条件得到MH的长即为点M到平面AB1N的距离,然后在直角三角形AME中,求出MH即可.
解答:解:(1)∵在直三棱柱ABC-A1B1C1中,AA1=2,AB=AC=1,∠BAC=90°,点M为BC中点,
∴AM⊥BC,AM⊥面BCC1B1
∴AM⊥MN,NM⊥AB1;AM∩AB1=A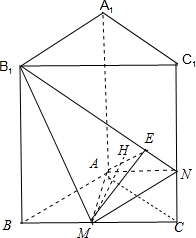
所以MN⊥AB1M
BC=B1C1=
,
设CN=x,则NC1=2-x
B1C12+NC12=B1M2+NM2
2+(2-x)2=22+(
)2+(
)2+x2,
解得x=
.
(2)∵AB∥A1B1
∴异面直线B1N与AB所成的角为∠A1BN
∵面ABB1A1⊥面ACC1A1,
∴B1A1⊥面ACC1A1,B1A1⊥A1N
A1N=
=
=
.
∴tan∠A1BN=
=
.
(3)连接AM,M为BC中点,∴AM⊥BC,AM⊥面BCC1B1
作ME⊥B1N,交B1N于E,连接AE,∴AE⊥B1N (三垂线定理)
∴∠AEM为二面角A--B1N-M的平面角
B1N2=22+
+(
)2=
⇒B1N=
.
NM2=
+(
)2
设EN=x,∵△B1NM为直角三角形,∴NM2=x•B1N
即
=
⇒x=
.
ME=
=
AM=
,
∴tan∠AEM=
=1
∴二面角A-B1N-M为45°.
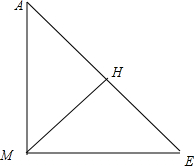
(4)作MH⊥AE于H,①
由第三问得B1N⊥平面AEM,所以B1N⊥MH,②
AE∩B1N=E ③
结合①②③得:MH⊥平面AB1N;
∴MH的长即为点M到平面AB1N的距离
在直角三角形AME中,MH=MEsin∠AEM=MEsin45°=
×
=
.
即点M到平面AB1N的距离为:
.
∴AM⊥BC,AM⊥面BCC1B1
∴AM⊥MN,NM⊥AB1;AM∩AB1=A

所以MN⊥AB1M
BC=B1C1=
| 2 |
设CN=x,则NC1=2-x
B1C12+NC12=B1M2+NM2
2+(2-x)2=22+(
| 1 |
| 2 |
| 1 |
| 2 |
解得x=
| 1 |
| 4 |
(2)∵AB∥A1B1
∴异面直线B1N与AB所成的角为∠A1BN
∵面ABB1A1⊥面ACC1A1,
∴B1A1⊥面ACC1A1,B1A1⊥A1N
A1N=
| A1C1 2+C1N2 |
1+(
|
| ||
| 4 |
∴tan∠A1BN=
| A1N |
| A1B1 |
| ||
| 4 |
(3)连接AM,M为BC中点,∴AM⊥BC,AM⊥面BCC1B1
作ME⊥B1N,交B1N于E,连接AE,∴AE⊥B1N (三垂线定理)
∴∠AEM为二面角A--B1N-M的平面角
B1N2=22+
| 1 |
| 2 |
| 1 |
| 4 |
| 81 |
| 16 |
| 9 |
| 4 |
NM2=
| 1 |
| 2 |
| 1 |
| 4 |
设EN=x,∵△B1NM为直角三角形,∴NM2=x•B1N
即
| 9 |
| 16 |
| 9x |
| 4 |
| 1 |
| 4 |
ME=
| MN2-EN2 |
| ||
| 2 |
AM=
| ||
| 2 |

∴tan∠AEM=
| AM |
| EM |
∴二面角A-B1N-M为45°.
(4)作MH⊥AE于H,①
由第三问得B1N⊥平面AEM,所以B1N⊥MH,②
AE∩B1N=E ③
结合①②③得:MH⊥平面AB1N;
∴MH的长即为点M到平面AB1N的距离
在直角三角形AME中,MH=MEsin∠AEM=MEsin45°=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
即点M到平面AB1N的距离为:
| 1 |
| 2 |
点评:本题主要考察二面角的平面角及求法以及异面直线及其所成的角和点到面的距离计算,是对立体几何知识的综合考察,难度较高,综合性强.

练习册系列答案
相关题目




