题目内容
已知函数f(x)=x2+(a-1)x+b,f(1)=1(1)若函数f(x)没有零点,求a的取值范围;
(2)若函数f(x)的图象的对称轴是x=1,解不等式f(x)>5.
【答案】分析:(1)函数f(x)没有零点,即△=(a-1)2-4b<0,又据f(1)=1,a+b=1,消去b得出关于a的不等式求解
(2)函数f(x)的图象的对称轴是x=1,求得a=-1,b=2,f(x)>5即为x2-2x-3>0.
解答:解:(1)由f(1)=1得1+a-1+b=1,a+b=1
若函数f(x)没有零点,则△=(a-1)2-4b<0,又b=1-a,所以a2-2a+1-4(1-a)<0,解得-3<a<1
(2)函数f(x)的图象的对称轴是x=1,即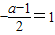 ,a-1=-2,a=-1,b=2
,a-1=-2,a=-1,b=2
f(x)=x2-2x+2>5,即x2-2x-3>0,解得x<-1,或x>3
所以不等式f(x)>5的解集为{x|x<-1,或x>3}
点评:本题考查二次函数的图象与性质,二次不等式求解,体现了数形结合,转化的思想方法.
(2)函数f(x)的图象的对称轴是x=1,求得a=-1,b=2,f(x)>5即为x2-2x-3>0.
解答:解:(1)由f(1)=1得1+a-1+b=1,a+b=1
若函数f(x)没有零点,则△=(a-1)2-4b<0,又b=1-a,所以a2-2a+1-4(1-a)<0,解得-3<a<1
(2)函数f(x)的图象的对称轴是x=1,即
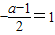 ,a-1=-2,a=-1,b=2
,a-1=-2,a=-1,b=2f(x)=x2-2x+2>5,即x2-2x-3>0,解得x<-1,或x>3
所以不等式f(x)>5的解集为{x|x<-1,或x>3}
点评:本题考查二次函数的图象与性质,二次不等式求解,体现了数形结合,转化的思想方法.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|