题目内容
已知数列{an}是非常值数列的等差数列,Sn为其前n项和,S5=25,且a1,a3,a13成等比数列;(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| 2 | an+1 |
分析:(1)利用等差数列的通项公式表示出相应的项,待定系数法设出首项和公差,根据S5=25,a1,a3,a13成等比数列列出关于首项和公差的方程组,通过求解该方程组求出首项和公差,进而写出该数列的通项公式;
(2)根据数列{an}的通项公式写出数列{bn}的通项公式,令An=T2n-Tn=
+
+…+
,利用作差法,判断数列{An}的单调性,从而求得
T2n-Tn≥t对一切正整数n恒成立时实数t的范围.
(2)根据数列{an}的通项公式写出数列{bn}的通项公式,令An=T2n-Tn=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
T2n-Tn≥t对一切正整数n恒成立时实数t的范围.
解答:解:(Ⅰ)设{an}的公差为d,S5=
•5=
•5=a3•5=25,
∴a3=5.
a1,a3,a13成等比数列.则25=(5-2d)(5+10d),解得d=2,d=0(舍).
an=a3+(n-3)d=5+(n-3)•2=2n-1.
数列{an}的通项公式an=2n-1,n∈N*.
(Ⅱ)bn=
=
=
,Tn=1+
+
+…+
,
令An=T2n-Tn=
+
+…+
,
则An+1-An=(
+
+…+
)-(
+
+…+
)
=-
+
+
=-
+
>0,∴An≥A1=
.
实数t的取值范围为:t≤
| a1+a5 |
| 2 |
| 2•a3 |
| 2 |
∴a3=5.
a1,a3,a13成等比数列.则25=(5-2d)(5+10d),解得d=2,d=0(舍).
an=a3+(n-3)d=5+(n-3)•2=2n-1.
数列{an}的通项公式an=2n-1,n∈N*.
(Ⅱ)bn=
| 2 |
| an+1 |
| 2 |
| 2n-1+1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
令An=T2n-Tn=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
则An+1-An=(
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
=-
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| 2n+2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
实数t的取值范围为:t≤
| 1 |
| 2 |
点评:本题考查待定系数法,考查学生对等差数列通项公式的理解能力,以及利用作差法判定数列的单调性,体现了数列的函数特性,同时考查了运算能力,属难题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 ,Tn为数列{bn}的前n项和,若T2n-Tn≥t对一切正整数n恒成立,求实数t的范围.
,Tn为数列{bn}的前n项和,若T2n-Tn≥t对一切正整数n恒成立,求实数t的范围.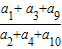 的值是 .
的值是 .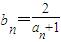 ,Tn为数列{bn}的前n项和,若T2n-Tn≥t对一切正整数n恒成立,求实数t的范围.
,Tn为数列{bn}的前n项和,若T2n-Tn≥t对一切正整数n恒成立,求实数t的范围.