题目内容
已知数列{an}是非零等差数列，又a1，a3，a9组成一个等比数列的前三项，则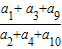
的值是 ．
【答案】分析：设等差数列的公差为d，利用a1，a3，a9组成一个等比数列的前三项及d≠0，求得d=a1，由此即可求得结论．
解答：解：设等差数列的公差为d，则
∵a1，a3，a9组成一个等比数列的前三项
∴（a1+2d）2=a1（a1+8d）
∴d2=a1d
∵d≠0
∴d=a1，
∴
=
=
故答案为：
点评：本题考查等比数列的性质，考查等差数列的通项，正确运用等比数列的性质是关键．
解答：解：设等差数列的公差为d，则
∵a1，a3，a9组成一个等比数列的前三项
∴（a1+2d）2=a1（a1+8d）
∴d2=a1d
∵d≠0
∴d=a1，
∴
==故答案为：
点评：本题考查等比数列的性质，考查等差数列的通项，正确运用等比数列的性质是关键．
练习册系列答案
相关题目
，Tn为数列{bn}的前n项和，若T2n-Tn≥t对一切正整数n恒成立，求实数t的范围．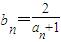
，Tn为数列{bn}的前n项和，若T2n-Tn≥t对一切正整数n恒成立，求实数t的范围．