题目内容
求过两点A(1,4)、B(3,2)且圆心在直线y=0上的圆的标准方程,并判断点P(2,4)与圆的关系.
解:(解法1)(待定系数法)设圆的标准方程为(x-a)2+(y-b)2=r2.
∵ 圆心在y=0上,故b=0.
∴ 圆的方程为(x-a)2+y2=r2.
∵ 该圆过A(1,4)、B(3,2)两点,
∴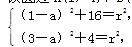 解之得a=-1,r2=20.
解之得a=-1,r2=20.
∴ 所求圆的方程为(x+1)2+y2=20.
(解法2)(直接求出圆心坐标和半径)∵ 圆过A(1,4)、B(3,2)两点,∴ 圆心C必在线段AB的垂直平分线l上.∵ kAB= =-1,故l的斜率为1,又AB的中点为(2,3),故AB的垂直平分线l的方程为y-3=x-2即x-y+1=0.又知圆心在直线y=0上,故圆心坐标为C(-1,0).∴ 半径r=|AC|=
=-1,故l的斜率为1,又AB的中点为(2,3),故AB的垂直平分线l的方程为y-3=x-2即x-y+1=0.又知圆心在直线y=0上,故圆心坐标为C(-1,0).∴ 半径r=|AC|= =
= .故所求圆的方程为(x+1)2+y2=20.又点P(2,4)到圆心C(-1,0)的距离为d=|PC|=
.故所求圆的方程为(x+1)2+y2=20.又点P(2,4)到圆心C(-1,0)的距离为d=|PC|= =
= >r.
>r.
∴ 点P在圆外.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 都是锐角,且
都是锐角,且 ,
, ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,则
,则 B.若
B.若 ,则
,则
 ,则
,则 ,
, 。
。 的极值;
的极值; (
( )上存在一点
)上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围。
的取值范围。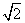 PN,试建立适当的坐标系,并求动点P的轨迹方程.
PN,试建立适当的坐标系,并求动点P的轨迹方程.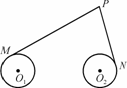

 的顶点
的顶点 在底面
在底面 内射影为
内射影为 (在
(在 内部,即过
内部,即过 底面
底面 时,则
时,则 中点 D.重心
中点 D.重心 在
在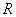 上有定义,对于给定的正数
上有定义,对于给定的正数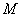 ,定义函数
,定义函数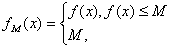 ,取函数
,取函数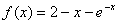 ,若对任意的
,若对任意的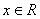 恒有
恒有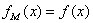 ,则:( )
,则:( )