题目内容
已知等差数列{an}的前n项的和记为Sn．如果a4＝－12，a8＝－4．
(1)求数列{an}
的通项公式；
(2)求Sn的最小值及其相应的n的值；
(1)求数列{an}
的通项公式；(2)求Sn的最小值及其相应的n的值；
解：（１）设数列
的首项为
，公差为
．则有
解得
所以数列的通项公式为
（２）当
时，由
及
得
当
时， 由
①
知
②
①-②得：
即：
因此，数列
是等比数列，首项为
，公比为
。
（3）由（2）知数列是等比数列，且首项为，公比为。
①
②
①－②得
的首项为，公差为．则有 解得所以数列
的通项公式为（２）当
时，由及得当
时， 由①知
②①-②得：
即：
因此，数列
是等比数列，首项为，公比为。（3）由（2）知数列
是等比数列，且首项为，公比为。①②①－②得
略
练习册系列答案
相关题目
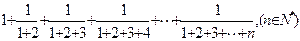
，且
，则
（ ）
的首项
，
前n项和为
，且
，且数列
的前n项和
。
的前
项和
，则数列
中数值最小的项是第_项.
三个字母组成一个长度为
个字母的字符串，要求由
开始，相邻两个字母不同. 例如
时，排出的字符串可能是
或
；
时排出的字符串可能是
，
（如图）.若记这种
， 可知，
；则
___________；数列
的前
项之和
__________．