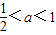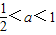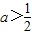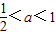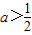题目内容
若函数y=(2a-1)x在R上为单调减函数,那么实数a的取值范围是
- A.a>1
- B.

- C.a≤1
- D.

B
分析:指数函数y=ax,当0<a<1时为定义域上的减函数,故依题意只需0<2a-1<1,即可解得a的范围
解答:函数y=(2a-1)x在R上为单调减函数,
∴0<2a-1<1
解得 <a<1
<a<1
故选 B
点评:本题主要考查了指数函数的单调性,通过底数判断指数函数单调性的方法,属基础题
分析:指数函数y=ax,当0<a<1时为定义域上的减函数,故依题意只需0<2a-1<1,即可解得a的范围
解答:函数y=(2a-1)x在R上为单调减函数,
∴0<2a-1<1
解得
 <a<1
<a<1故选 B
点评:本题主要考查了指数函数的单调性,通过底数判断指数函数单调性的方法,属基础题

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目