题目内容
(本题满分12分)已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0,②f(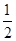 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),
都有f(xy)= f(x)+ f(y),求不等式f(x)+ f(5-x)≥-2的解集。
 。
。
解析试题分析:(1)构造函数中两个任意变量的函数值差,结合函数表达式得到函数单调性的证明。
(2)结合特殊值的函数值,得到f(4)=-2,进而得到函数的不等式的求解。
解:设0<x1<x2,则 >1,∵f(xy)= f(x)+ f(y)
>1,∵f(xy)= f(x)+ f(y)
∴f(x2)= f(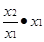 )= f(
)= f( )+ f(x1)
)+ f(x1)
又∵x>1时,f(x)<0,∴f( )<0
)<0
∴f(x2)<f(x1),∴f(x)是( 0,+∞)上的减函数。又∵f(1)= f(1)+ f(1)
∴f(1)=0,而f(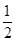 )=1,∴f(2?
)=1,∴f(2?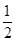 )= f(2)+ f(
)= f(2)+ f(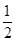 )=0
)=0
∴f(2)=-1,∴f(x)+ f(5-x)≥-2="2" f(2)= f(4)
∴ ,∴0<x≤1,或4≤x<5
,∴0<x≤1,或4≤x<5
∴原不等式的解集是 。
。
考点:本题主要考查了函数的单调性的运用。
点评:解决该试题的关键是能利用已知条件分析得到函数的单调性的证明,结合已知的关系式将所求的表示为一个整体函数式,同时能结合单调性得到求解。

练习册系列答案
相关题目
 为奇函数,
为奇函数, 为常数.
为常数. 在区间
在区间 内单调递增;
内单调递增; 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
,  ,求:
,求: 的定义域。 (2)求使
的定义域。 (2)求使 的
的 的取值范围。
的取值范围。 .
. 在
在 上是单调递增函数;
上是单调递增函数; 时,求函数在
时,求函数在 上的最值;
上的最值; 上恒有
上恒有 成立,求
成立,求 的取值范围.
的取值范围. 的函数
的函数 同时满足:
同时满足: ,总有
,总有 ; ②
; ② ;
; ,则有
,则有 成立。
成立。 的值;
的值; ,总有
,总有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 为奇函数;
为奇函数; 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.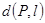 。
。 ,线段
,线段 ,求
,求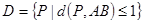 所表示图形的面积;
所表示图形的面积; 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分) 是R上的偶函数,且当
是R上的偶函数,且当 时,函数解析式为
时,函数解析式为 ,
, 的值;
的值; 时,函数的解析式。
时,函数的解析式。 的定义域;
的定义域; 的值域;
的值域;