题目内容

3．不等式1≤|3x+4|＜6的解集是（-$\frac{10}{3}$，-$\frac{5}{3}$]∪[-1，$\frac{2}{3}$）．

分析 将不等式1≤|3x+4|＜6转化为不等式组，解出即可．

解答 解：∵1≤|3x+4|＜6，
∴$\left\{\begin{array}{l}{3x+4≥1}\\{-6＜3x+4＜6}\end{array}\right.$或$\left\{\begin{array}{l}{3x+4≤-1}\\{-6＜3x+4＜6}\end{array}\right.$，
解得：-1≤x＜$\frac{2}{3}$或-$\frac{10}{3}$＜x≤-$\frac{5}{3}$，
故答案为：（-$\frac{10}{3}$，-$\frac{5}{3}$]∪[-1，$\frac{2}{3}$）．

点评 本题考查了绝对值不等式的解法，属于基础题．

练习册系列答案
相关题目
13．求圆的极坐标方程：
（1）圆心在A（1，$\frac{π}{4}$），半径为1的圆；
（2）圆心在（a，$\frac{π}{2}$），半径为a的圆．
14．已知函数f（x）=sinωxcosωx+$\sqrt{3}$cos2ωx+$\frac{3}{2}$（ω＞0），其两条相邻对称轴之间的距离等于$\frac{π}{2}$．
（Ⅰ）求f（x）的解析式
（Ⅱ）若对?x∈[-$\frac{π}{12}$，0]，都有|f（x）-m|≤1，求实数m的取值范围．
11．已知在△ABC中，2sinA=$\sqrt{3}$sinC-sinB，则A的取值范围为$[\frac{π}{6}，\frac{π}{2}]$．
18．a，b≥1，a≠b，下列各数中最大的是（　　）
A．$\frac{1}{2}$（a+b）B．$\frac{2ab}{a+b}$C．$\frac{1}{2}$（$\frac{1}{a}$+$\frac{1}{b}$）D．$\sqrt{ab}$
8．解方程组：$\left\{\begin{array}{l}{（a-1）^{2}+{b}^{2}=（1+r）^{2}}\\{（3-a）^{2}+（-\sqrt{3}-b）^{2}={r}^{2}}\\{（a+\sqrt{3}b）^{2}=4{r}^{2}}\end{array}\right.$．（r＞0）
15．已知实数x1，x2，…，x10满足$\sum_{i=1}^{10}$|xi-1|≤4，$\sum_{i=1}^{10}$|xi-2|≤6，求x1，x2，…，x10的平均值．
17．已知函数f（x）=e|x|+|x-a|是偶函数．
（Ⅰ）求曲线y=f（x）在x=1处的切线方程；
（Ⅱ）求不等式f（x）≥x的解集．
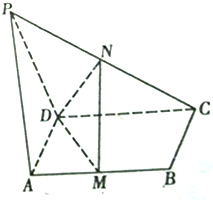18．如图，已知PA⊥平面ABCD，ABCD为矩形，M、N为AB、PC的中点．
（1）求证：MN⊥AB；
（2）若平面PDC与平面ABCD成45°角，求证：平面MND⊥平面PDC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网