题目内容
已知定义在 上的偶函数
上的偶函数 满足:
满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:
单调递减,给出以下四个命题:
① ;
;
② 为函数
为函数 图像的一条对称轴;
图像的一条对称轴;
③函数 在
在 单调递增;
单调递增;
④若关于 的方程
的方程 在
在 上的两根
上的两根 ,则
,则 .
.
以上命题中所有正确的命题的序号为_______________.
【答案】
①②④
【解析】
试题分析:∵ ,∴当
,∴当 时,
时, ,∴
,∴ ,
,
又∵函数 是偶函数,∴
是偶函数,∴ ,∴①正确;∵
,∴①正确;∵ ,
, ,
,
∴ ,∴
,∴ ,又
,又 是函数
是函数 图像的对称轴,∴
图像的对称轴,∴ 是函数
是函数 图像的对称轴,∴②正确;∵函数
图像的对称轴,∴②正确;∵函数 的周期是4,∴
的周期是4,∴ 在
在 上的单调性与
上的单调性与 上的单调性相同,∴
上的单调性相同,∴ 在
在 上为减函数,∴③错误;∵
上为减函数,∴③错误;∵ 是函数
是函数 图像的对称轴,∴方程
图像的对称轴,∴方程 的两根关于
的两根关于 对称,∴
对称,∴ ,∴④正确.
,∴④正确.
考点:1.函数的周期性;2.函数的奇偶性;3.函数的对称性;4.函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的偶函数满足:
上的偶函数满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:①
单调递减,给出以下四个命题:① ;②
;② 是函数
是函数 上单调递增;④若方程
上单调递增;④若方程 .在区间
.在区间 上有两根为
上有两根为 ,则
,则 。以上命题正确的是 。(填序号)
。以上命题正确的是 。(填序号) 上的偶函数
上的偶函数 的周期为2,且当
的周期为2,且当 时,
时, ,则
,则 .
. 上的偶函数
上的偶函数 满足
满足 ,且在区间[0,2]上
,且在区间[0,2]上 ,若关于
,若关于 的方程
的方程 有三个不同的根,则
有三个不同的根,则 的范围为
的范围为 B.
B. C.
C. D.
D.
 上的偶函数
上的偶函数 是满足:①
是满足:①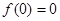 ;②
;② 上单调递减;③当
上单调递减;③当 时,
时, 。则
。则 的大小关系是
的大小关系是