题目内容
6.△ABC的内角A,B,C所对的边为a,b,c,其中a=1,b=$\sqrt{3}$,A=30°,则①B=60°;
②△ABC的面积为$\frac{\sqrt{3}}{2}$;
③△ABC外接圆的面积为4π;
④△ABC内切圆的半径为$\frac{\sqrt{3}-1}{2}$.
其中所有叙述中正确的个数有0个.
分析 对四个选项分别进行判断,即可得出结论.
解答 解:①∵a=1,b=$\sqrt{3}$,A=30°,
∴$\frac{1}{sin30°}=\frac{\sqrt{3}}{sinB}$,
∴sinB=$\frac{\sqrt{3}}{2}$,
∵b>a,
∴B>A,
∴B=60°或120°,故不正确;
②由①可知△ABC的面积有2个值,故不正确;
③设△ABC外接圆的半径为R,则2R=$\frac{1}{sin30°}$=2,∴R=1,∴△ABC外接圆的面积为π,故不正确;
④由②可知,△ABC内切圆的半径有两个值.
故答案为:0.
点评 本题考查正弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
16.下列函数是幂函数的是( )
| A. | y=2x2 | B. | y=x3+x | C. | y=3x | D. | y=x3 |
17.将参数方程$\left\{\begin{array}{l}x=-2+{cos^2}θ\\ y={cos^2}θ\end{array}\right.$(θ为参数)化为普通方程为( )
| A. | y=x-2 | B. | y=x-2(0≤y≤1) | C. | y=x+2(-2≤x≤-1) | D. | y=x+2 |
14.已知直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=t}\end{array}\right.$ (t为参数),圆C的极坐标方程为ρ=2cos θ,则圆C的圆心到直线l的距离为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
16.已知U={三角形},A={锐角三角形},B={钝角三角形},则∁UA∩B=( )
| A. | {锐角三角形} | B. | {钝角三角形} | C. | {直角三角形} | D. | {三角形} |
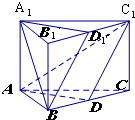 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.