题目内容
【题目】已知等比数列
的前
项和为
，公比
， 
， 
．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设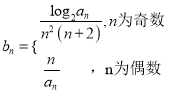
， 
为{
}的前
项和，求
．
【答案】(Ⅰ) 
；(Ⅱ) 
.
【解析】试题分析：
(Ⅰ)由题意求得数列的首项、公比均为2，则数列的通项公式为an=2n；
(Ⅱ)由题意裂项求和可得
.
试题解析：
（I）∵等比数列{an}的前n项和为Sn，公比q＞0，S2=2a2﹣2，S3=a4﹣2．
∴a3=a4﹣2a2，可得a2q=a2（q2﹣2），
∴q2﹣q﹣2=0，解得q=2．∴a1+a2=2a2﹣2，即a1=a2﹣2=2a1﹣2，解得a1=2．
∴an=2n．
（II）n为奇数时，bn=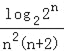
=
=
．
n为偶数时，bn=
．
∴T2n=
+
+…+
+
+…+
=
+
+…+
=
++…+．
设A=+…+
，
则
A=
+…+
+
，
∴
A=
+…+
﹣
=
﹣，
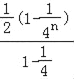∴A=
﹣
．
∴T2n=
+﹣．
练习册系列答案
相关题目
