题目内容
已知曲线C:y=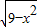 ,与直线l:y=x+b没有公共点,则( )
,与直线l:y=x+b没有公共点,则( )A.|b|≥3
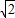
B.0<b<
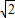
C.-3≤b≤3
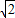
D.b>3
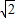 或b<-3
或b<-3
【答案】分析:曲线C:y=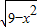 表示圆心为原点,半径为3的x轴上方的半圆,画出两函数的图象,根据圆与直线没有公共点,抓住两个关键点:1是找出直线l与圆O相切时b的值;2是找出直线l过B时b的值,利用函数图象即可得到曲线C与直线l没有公共点时b的范围.
表示圆心为原点,半径为3的x轴上方的半圆,画出两函数的图象,根据圆与直线没有公共点,抓住两个关键点:1是找出直线l与圆O相切时b的值;2是找出直线l过B时b的值,利用函数图象即可得到曲线C与直线l没有公共点时b的范围.
解答: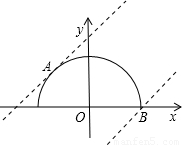 解:当曲线C与直线l相切时,圆心(0,0)到y=x+b的距离d=r,
解:当曲线C与直线l相切时,圆心(0,0)到y=x+b的距离d=r,
即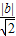 =3,解得:b=3
=3,解得:b=3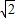 或b=-3
或b=-3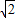 (舍去);
(舍去);
当直线l过(3,0)时,将(3,0)代入直线方程得:3+b=0,解得:b=-3,
则由图形可得出曲线C与直线l没有公共点时,b的范围为b>3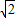 或b<-3.
或b<-3.
故选D
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,以及圆的标准方程,利用了数形结合的思想,数形结合思想是数学中重要的思想方法,做题时注意灵活运用.
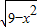 表示圆心为原点,半径为3的x轴上方的半圆,画出两函数的图象,根据圆与直线没有公共点,抓住两个关键点:1是找出直线l与圆O相切时b的值;2是找出直线l过B时b的值,利用函数图象即可得到曲线C与直线l没有公共点时b的范围.
表示圆心为原点,半径为3的x轴上方的半圆,画出两函数的图象,根据圆与直线没有公共点,抓住两个关键点:1是找出直线l与圆O相切时b的值;2是找出直线l过B时b的值,利用函数图象即可得到曲线C与直线l没有公共点时b的范围.解答:
 解:当曲线C与直线l相切时,圆心(0,0)到y=x+b的距离d=r,
解:当曲线C与直线l相切时,圆心(0,0)到y=x+b的距离d=r,即
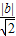 =3,解得:b=3
=3,解得:b=3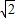 或b=-3
或b=-3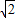 (舍去);
(舍去);当直线l过(3,0)时,将(3,0)代入直线方程得:3+b=0,解得:b=-3,
则由图形可得出曲线C与直线l没有公共点时,b的范围为b>3
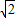 或b<-3.
或b<-3.故选D
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,以及圆的标准方程,利用了数形结合的思想,数形结合思想是数学中重要的思想方法,做题时注意灵活运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 =0与D有公共点,试求a的最小值.
=0与D有公共点,试求a的最小值.