题目内容
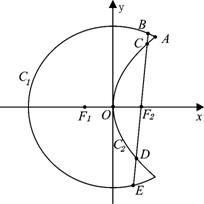
如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点,且
的交点,且![]() 为钝角,若
为钝角,若![]() ,
,![]() .(Ⅰ)求曲线
.(Ⅰ)求曲线![]() 和
和![]() 所在的椭圆和抛物线方程;
所在的椭圆和抛物线方程;
(Ⅱ)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,证明
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,证明![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
解:(Ⅰ)设椭圆方程为![]() ,
,
则![]()
![]() ,
,![]() ………2分
………2分
设![]() ,则
,则![]() ,
,![]() ,两式相减得
,两式相减得![]() ,由抛物线定义可知
,由抛物线定义可知![]() ,则
,则![]() 或
或![]() (舍去)
(舍去)
所以椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() . ……5分
. ……5分
(Ⅱ)设![]() ,直线
,直线![]() ,代入
,代入![]()
得:![]() ,即
,即![]() ,
,
![]() ……………7分
……………7分
同理,将![]() 代入
代入![]() 得:
得:![]() ,
,![]() ,…9分
,…9分
所以![]() =
=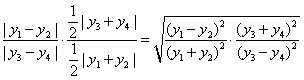
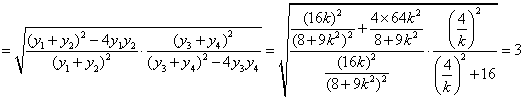 为定值
为定值

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
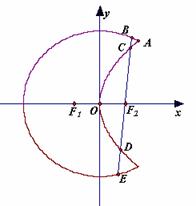
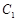 是以原点O为中心、
是以原点O为中心、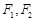 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线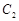 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线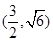 且
且 为钝角.
为钝角. 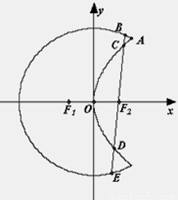
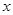 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线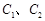 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由. 是以原点O为中心、
是以原点O为中心、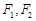 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线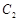 是以O为顶点、
是以O为顶点、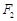 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若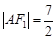 ,
,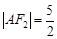 .
. 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问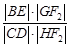 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由. 是以原点O为中心、
是以原点O为中心、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若 ,
, .
. 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
 是以原点O为中心、
是以原点O为中心、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若 ,
,
 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由
是否为定值?若是求出定值;若不是说明理由