题目内容
如图在![]() 中,三个顶点坐标分别为
中,三个顶点坐标分别为![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 过
过![]() 点且曲线
点且曲线![]() 上任一点
上任一点![]() 满足
满足![]() 是定值.
是定值.
(Ⅰ)求出曲线![]() 的标准方程;
的标准方程;
(Ⅱ)设曲线![]() 与
与![]() 轴,
轴,![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() ,
,
是否存在斜率为![]() 的直线
的直线![]() 过定点
过定点![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且向量
,且向量![]() 与
与![]() 共线.若存在,求出此直线方程;若不存在,请说明理由.
共线.若存在,求出此直线方程;若不存在,请说明理由.
 |
解:(I)由题设得![]()
![]()
又![]() 是定值 ∴
是定值 ∴![]()
由椭圆定义,点P的轨迹是以A、B为焦点的椭圆.
![]()
![]()
![]()
椭圆E方程 ![]()
(II)由已知条件l方程为![]()
 消去y整理得
消去y整理得
![]()
l与椭圆有2个不同交点的条件为△![]()
解得![]() 或
或![]()
若l与椭圆交于![]()
![]()
![]()
![]()
椭圆与x轴,y轴交点![]() ,
,![]() ,
,![]()
![]() 与
与![]() 共线
共线
∴![]()
![]() 解得
解得![]()
![]()
∴不存在符合题设条件的直线l.

练习册系列答案
相关题目
 如图在Rt△ABC中,三个顶点坐标分别为A(-1,0),B(1,0),
如图在Rt△ABC中,三个顶点坐标分别为A(-1,0),B(1,0),

 中,三个顶点坐标分别为
中,三个顶点坐标分别为 ,
, ,
, ,曲线
,曲线 过
过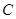 点且曲线
点且曲线 满足
满足 是定值.
是定值. 轴,
轴, 轴的交点分别为
轴的交点分别为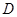 、
、 ,
, 的直线
的直线 过定点
过定点 与曲线
与曲线 、
、 ,且向量
,且向量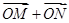 与
与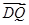 共线.若存在,求出此直线方程;若不存在,请说明理由.
共线.若存在,求出此直线方程;若不存在,请说明理由.