题目内容
已知x2+y2-2ax+4y-6=0的圆心在直线x+2y+1=0上,那么实数a等于 .
【答案】分析:根据所给的圆的一般式方程,看出圆的圆心,根据圆心在一条直线上,把圆心的坐标代入直线的方程,得到关于a的方程,解方程即可.
解答:解:∵x2+y2-2ax+4y-6=0的圆心是(a,-2),
圆心在直线x+2y+1=0上,
∴a+2(-2)+1=0,
∴a=3
故答案为:3
点评:本题考查圆的一般方程与点与直线的位置关系,本题解题的关键是表示出圆心,根据圆心的位置,写出符合条件的方程,本题是一个基础题.
解答:解:∵x2+y2-2ax+4y-6=0的圆心是(a,-2),
圆心在直线x+2y+1=0上,
∴a+2(-2)+1=0,
∴a=3
故答案为:3
点评:本题考查圆的一般方程与点与直线的位置关系,本题解题的关键是表示出圆心,根据圆心的位置,写出符合条件的方程,本题是一个基础题.

练习册系列答案
相关题目
 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为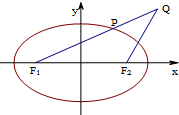 已知椭圆
已知椭圆