题目内容

设椭圆的两个焦点分别为F_1、、F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

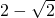
D
分析：设点P在x轴上方，坐标为 $\text{[math]}$ ，根据题意可知|PF₂|= $\text{[math]}$ ，|PF₂|=|F₁F₂|，，进而根据 $\text{[math]}$ 求得a和c的关系，求得离心率．
解答：设点P在x轴上方，坐标为 $\text{[math]}$ ，
∵△F₁PF₂为等腰直角三角形
∴|PF₂|=|F₁F₂|，即 $\text{[math]}$ ，即 $\text{[math]}$
故椭圆的离心率e= $\text{[math]}$
故选D
点评：本题主要考查了椭圆的简单性质．椭圆的离心率是高考中选择填空题常考的题目．应熟练掌握圆锥曲线中a，b，c和e的关系．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

设椭圆的两个焦点分别为F₁、F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是（　　）

设椭圆的两个焦点分别为F₁，F₂，过F₂作椭圆长轴的垂线与椭圆相交，其中的一个交点为P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是（　　）

设椭圆的两个焦点分别为F₁，F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率为

设椭圆的两个焦点分别为F₁、F₂，椭圆短轴的一端点为B，若△F₁BF₂为等腰直角三角形，则椭圆的离心率是（　　）

10.设椭圆的两个焦点分别为

，过F₂作椭圆长轴的垂线交椭圆于点

为等腰直角三角形，则椭圆的离心率为（）

A B

C D